Exam 8: Estimation of the Mean and Proportion
Exam 1: Introduction50 Questions
Exam 2: Organizing and Graphing Data93 Questions
Exam 3: Numerical Descriptive Measures92 Questions
Exam 4: Probability75 Questions
Exam 5: Discrete Random Variables and Their Probability Distribution77 Questions
Exam 6: Continuous Random Variables and the Normal Distribution74 Questions
Exam 7: Sampling Distributions76 Questions
Exam 8: Estimation of the Mean and Proportion60 Questions
Exam 9: Hypothesis Tests About the Mean and Proportion93 Questions
Exam 10: Estimation and Hypothesis Testing: Two Populations45 Questions
Exam 11: Chi-Square Tests98 Questions
Exam 12: Analysis of Variance62 Questions
Exam 13: Simple Linear Regression105 Questions
Select questions type
An advisor to the mayor of a large city wants to estimate,within 2.450 minutes,the mean travel time to work for all employees who work within the city limits.He knows that the standard deviation of all travel times is 11.35 minutes.He also wants to achieve a 95% confidence interval.He will poll a random sample of city employees.How many employees should he poll?
Free
(Short Answer)
4.8/5  (33)
(33)
Correct Answer:
83
A researcher wants to make a 95% confidence interval for a population mean.She wants the margin of error to be within 1.9 of the population mean.The population standard deviation is 11.07.The sample size that will yield a margin of error within 1.9 of the population mean is:
Free
(Short Answer)
4.9/5  (39)
(39)
Correct Answer:
131
A sample of 20 elements produced a mean of 91.4 and a standard deviation of 11.16.Assuming that the population has a normal distribution,the 90% confidence interval for the population mean is:
Free
(Essay)
4.8/5  (43)
(43)
Correct Answer:
Part A: the lower limit is 87.09 (rounded to two decimal places) Part B: the upper limit is 95.71 (rounded to two decimal places)
The z value for a 85% confidence interval for the population mean with 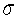 known is:
known is:
(Multiple Choice)
4.8/5  (46)
(46)
A sample of size 97 from a population having standard deviation 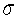 = 7 produced a mean of 47.The 99% confidence interval for the population mean (rounded to two decimal places)is:
= 7 produced a mean of 47.The 99% confidence interval for the population mean (rounded to two decimal places)is:
(Short Answer)
4.8/5  (41)
(41)
The margin of error for the population mean,assuming 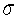 is known,is:
is known,is:
(Multiple Choice)
4.8/5  (37)
(37)
The value of t for 19 degrees of freedom and a 90% confidence interval is:
(Multiple Choice)
4.9/5  (37)
(37)
Which of the following conditions is required to use the t distribution to make a confidence interval for the population mean?
(Multiple Choice)
4.9/5  (32)
(32)
The mean federal income tax paid last year by a random sample of 45 persons selected from a city was $4,242.Suppose the standard deviation of tax paid in this city is 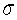 = $991.The 95% confidence interval for the population mean (rounded to two decimal places)is:
= $991.The 95% confidence interval for the population mean (rounded to two decimal places)is:
(Short Answer)
4.8/5  (36)
(36)
You are estimating the mean waiting time in line at a particular fast-food restaurant.You ask 30 customers,at varying times of the day,how long they waited in line before placing their order.You then take the average of these values and use this average to estimate the mean waiting time for all customers.The average of the 30 values is an example of a(n):
(Multiple Choice)
4.9/5  (39)
(39)
Which of the following is not an acceptable condition for using the t distribution to make a confidence interval for 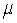 ?
?
(Multiple Choice)
4.9/5  (41)
(41)
Estimation is a procedure by which we assign a numerical value or numerical values to the:
(Multiple Choice)
4.7/5  (37)
(37)
A random sample of 8 houses selected from a city showed that the mean size of these houses is 1,881.0 square feet with a standard deviation of 328.00 square feet.Assuming that the sizes of all houses in this city have an approximate normal distribution,the 90% confidence interval for the mean size of all houses in this city,rounded to two decimal places,is:
(Short Answer)
4.8/5  (32)
(32)
A random sample of 12 life insurance policy holders showed that the mean value of their life insurance policies is $210,000 with a standard deviation of $44,600.Assuming that the values of life insurance policies for all such policy holders are approximately normally distributed,the 99% confidence interval for the mean value of all life insurance policies,rounded to two decimal places,is:
(Short Answer)
4.9/5  (34)
(34)
The confidence level of an interval estimate is denoted by:
(Multiple Choice)
4.9/5  (41)
(41)
The Eks Survey Company employs 2000 people to conduct telephone surveys.Because many people don't like to answer such surveys,many "hang-ups" (whereby the person hangs up without completing the survey)occur.The owner of Eks wants to determine the mean number of "hang-ups" per employee on a particular day,using 95% confidence.He samples 50 employees,and finds that the mean number of "hang-ups" on that day was 41.0.Suppose that the standard deviation of the number of "hang-ups" for all employees is 21.8 What is the value of the margin of error? (round to four decimal places)
(Short Answer)
4.9/5  (35)
(35)
A random sample of 82 customers,who visited a department store,spent an average of $71 at this store.Suppose the standard deviation of expenditures at this store is 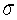 = $19.The 98% confidence interval for the population mean (rounded to two decimal places)is:
= $19.The 98% confidence interval for the population mean (rounded to two decimal places)is:
(Short Answer)
4.9/5  (29)
(29)
A sample of 25 elements produced a mean of 123.4 and a standard deviation of 18.32.Assuming that the population has a normal distribution,the 90% confidence interval for the population mean,rounded to two decimal places,is:
(Short Answer)
4.8/5  (34)
(34)
A researcher wants to make a 99% confidence interval for a population proportion.The most conservative estimate of the sample size that would limit the margin of error to be within 0.033 of the population proportion is:
(Short Answer)
4.7/5  (39)
(39)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)