Exam 8: Special Topics in Algebra
Exam 1: Functions, Graphs, and Models; Linear Functions306 Questions
Exam 2: Linear Models, Equations, and Inequalities212 Questions
Exam 3: Quadratic, Piecewise-Defined, and Power Functions261 Questions
Exam 4: Additional Topics With Functions299 Questions
Exam 5: Exponential and Logarithmic Functions304 Questions
Exam 6: Higher-Degree Polynomial and Rational Functions262 Questions
Exam 7: Systems of Equations and Matrices196 Questions
Exam 8: Special Topics in Algebra265 Questions
Select questions type
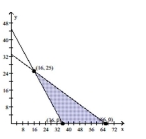
Use the given feasible region determined by the constraint inequalities to find the minimum possible value of the
objective function.
- subject to the constraints
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
B
Find the center and radius of the circle with the given equation.
-
(Multiple Choice)
4.8/5  (40)
(40)
Use the given feasible region determined by the constraint inequalities to find the minimum possible value of the
objective function.
-Find the maximum possible value of subject to the following constraints:
(Multiple Choice)
4.8/5  (28)
(28)
A nuclear cooling tower cross section is a hyperbola having a diameter of 56 ft at the center. The distance between the two foci is 100 ft. What is the equation for the hyperbola?
(Multiple Choice)
4.8/5  (40)
(40)
Eloise contracts to work for 10 days, receiving $0.03 the first day, $0.09 the second day, $0.27 the third day, and so on, with each day's pay triple that of the previous day. How much will she earn on the last day of the
Contract?
(Multiple Choice)
4.7/5  (43)
(43)
Round your answer to the nearest cent.
-Find the 7-year future value of an ordinary annuity with a contribution of $100 per year into an account that pays 6% per year, compounded annually.
(Multiple Choice)
4.9/5  (40)
(40)
Use negative exponents where necessary to write the expression with all variables in the numerator of a term. That is,
write each term in the form c if the term contains a variable.
-
(Multiple Choice)
4.8/5  (26)
(26)
Graph the solution set of the system of inequalities.
-A sushi restaurant charges $8.95 for its lunch buffet and $12.95 for its dinner buffet. In order for the restaurant to turn a profit, its buffets must generate daily revenue of at least $2190. Write an inequality that describes this
Requirement. Let x represent the number of lunch buffet customers and y represent the number of dinner buffet
Customers.
(Multiple Choice)
5.0/5  (40)
(40)
A certain club initially has 140 members and membership increases by 7 members every month. If dues are $20/month, what is the total amount of dues collected during the first year?
(Multiple Choice)
4.9/5  (38)
(38)
Find the next three terms of the arithmetic sequence.
-Find the eighth term of the arithmetic sequence with first term and common difference 4 .
(Multiple Choice)
4.8/5  (40)
(40)
An equation of the form can be thought of as the composition of the functions and u(x) ax k + b and can be written as where \(u = a x ^k + b. Use this concept to fill in the blanks.
-\[y = \sqrt [ 3 ] { ــــــــــــ } \text { can be written as } y = u ^ { - } \text {where } u ( x ) = 3 x ^ { 4 } + 2 x ^ { 3 } + 13\]
(Short Answer)
4.9/5  (27)
(27)
Find the sum of the first 10 terms of the arithmetic sequence with first term 11 and common difference -4 .
(Multiple Choice)
4.9/5  (34)
(34)
During the first day of an epidemic 8000 people get sick, during the second day 16,000 people get sick, and so on with the number of people getting sick increasing by 8000 each day. The epidemic peaks after 30 days with
8000 fewer people getting sick on the 31st day than on the 30th day, and so forth. What is the total number of
People who get sick?
(Multiple Choice)
4.8/5  (38)
(38)
Graph the solution region for the system of inequalities and identify the corners of the region.
-
(Multiple Choice)
4.7/5  (34)
(34)
A building has an entry with the shape of a parabolic arch 24 feet high and 4 feet wide at the base. Find an equation for the parabola if the vertex is placed at the origin of the coordinate system. 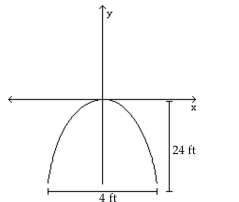
(Multiple Choice)
4.9/5  (27)
(27)
Rewrite the expression as a sum, difference, or multiple of logarithms.
-
(Multiple Choice)
4.9/5  (45)
(45)
Showing 1 - 20 of 265
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)