Exam 8: Trigonometric Identities and Equations
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
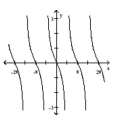
For the graph of a circular function y = f(x), determine whether f(-x) = f(x) or f(-x) = -f(x) is true.
-
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
A
Write the following as an algebraic expression in u, u > 0.
-The figure shows a stationary spy satellite positioned 15,000 miles above the equator. What percel to the nearest tenth, of the equator can be seen from the satellite? The diameter of Earth is 7927 miles at the equator.
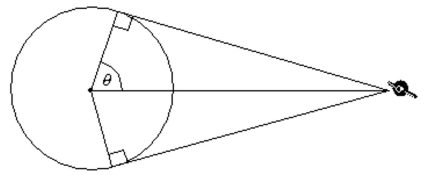
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
B
Provide an appropriate response.
-Explain what is wrong with the following solution for the equation in the interval .
2\theta= \theta= \theta= or \theta=
(Essay)
4.9/5  (40)
(40)
Write the expression in terms of sine and cosine, and simplify so that no quotients appear in the final expression.
-
(Multiple Choice)
4.9/5  (39)
(39)
Solve the equation for solutions in the interval [0 ). Round to the nearest degree.
-
(Multiple Choice)
4.8/5  (39)
(39)
Find the exact value of the expression using the provided information.
-Find given that , with in quadrant III, and , with in quadrant III.
(Multiple Choice)
4.9/5  (44)
(44)
Find the exact value of the expression using the provided information.
-Find given that , with in quadrant , and , with in quadrant IV.
(Multiple Choice)
4.9/5  (38)
(38)
Use an identity to write the expression as a single trigonometric function or as a single number.
-
(Multiple Choice)
4.8/5  (38)
(38)
Use identities to write the expression as a single function of x or
-
(Multiple Choice)
4.7/5  (29)
(29)
Solve the equation for solutions in the interval [0 ). Round to the nearest degree.
-
(Multiple Choice)
4.9/5  (37)
(37)
Use the fundamental identities to find the value of the trigonometric function.
-Find if and is in quadrant IV.
(Multiple Choice)
4.9/5  (32)
(32)
Determine all solutions of the equation in radians.
-Find , given that and terminates in .
(Multiple Choice)
4.8/5  (40)
(40)
Use a graphing calculator to make a conjecture as to whether each equation is an identity.
-
(Multiple Choice)
5.0/5  (37)
(37)
Showing 1 - 20 of 492
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)