Exam 7: Graph Theory
Exam 1: Critical Thinking67 Questions
Exam 2: Analysis of Growth70 Questions
Exam 3: Linear and Exponential Change: Comparing Growth Rates72 Questions
Exam 4: Personal Finance71 Questions
Exam 5: Introduction to Probability68 Questions
Exam 6: Statistics69 Questions
Exam 7: Graph Theory70 Questions
Exam 8: Voting and Social Choice70 Questions
Exam 9: Geometry70 Questions
Select questions type
If a circuit of a graph visits each vertex exactly once, then it is called a(n) _______________.
(Multiple Choice)
4.7/5  (39)
(39)
The graph below has two odd-degree vertices, so no Euler circuit exists. Suppose we would like to find a route that backtracks as little as possible. What duplicate edge could we create to help us find this route? 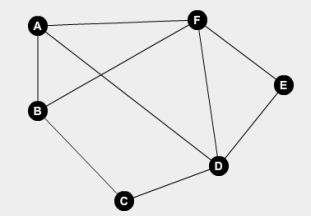
(Multiple Choice)
4.9/5  (30)
(30)
If each vertex of a graph is connected to every other vertex by an edge, then it is called a(n) _______________ graph.
(Multiple Choice)
4.9/5  (43)
(43)
One night you put a quarter into a slot machine and get back two quarters. The next night, you put these two quarters back in the machine one at a time, and each time two quarters came out. If you want to go home taking your winnings of $500, then what nights should this pattern be continued through?
(Multiple Choice)
4.8/5  (31)
(31)
Which of the following is not a practical situation where finding an Euler circuit may be important?
(Multiple Choice)
4.9/5  (41)
(41)
Use the cheapest link algorithm to find an approximate solution to the traveling salesman problem for the figure below. 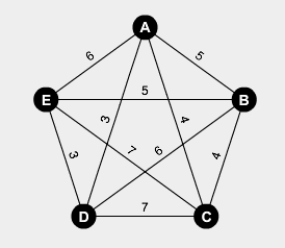
(Multiple Choice)
4.8/5  (48)
(48)
Use the nearest-neighbor algorithm starting at vertex A of the figure below to find an approximate solution to the traveling salesman problem. 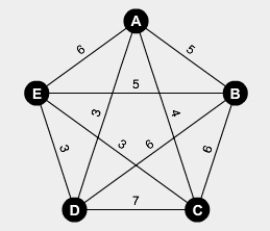
(Multiple Choice)
4.8/5  (35)
(35)
According to Euler's theorem, the figure below has an Euler circuit.
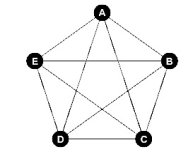
(True/False)
4.9/5  (41)
(41)
How many Euler circuits starting from the vertex B are possible? 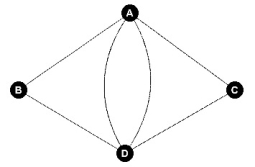
(Multiple Choice)
4.9/5  (37)
(37)
Suppose the edges of a certain graph represent phone lines that must be maintained, and the vertices represent junctions. A worker maintaining the lines would like to find an Euler circuit for this graph to increase ___________.
(Multiple Choice)
4.7/5  (29)
(29)
The edges in a certain graph represent roads, and the vertices represent intersections. We want to time the traffic signals at each intersection and not visit any intersection twice. Should we look for an Euler circuit or a Hamilton circuit?
(Multiple Choice)
4.9/5  (39)
(39)
In a complete binary tree of height H, the number of leaves equals _________.
(Multiple Choice)
4.7/5  (37)
(37)
Use the cheapest link algorithm to find an approximate solution to the traveling salesman problem for the figure below. 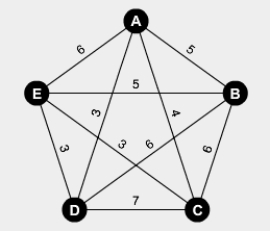
(Multiple Choice)
4.7/5  (31)
(31)
How many smaller circuits can be a part of a Hamilton circuit?
(Multiple Choice)
4.9/5  (29)
(29)
When applying the nearest-neighbor algorithm, if there are two or more vertices equally nearby, any one of them may be selected.
(True/False)
4.8/5  (39)
(39)
Showing 41 - 60 of 70
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)