Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution
Exam 1: Introduction36 Questions
Exam 2: An Introduction to Linear Programming46 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution36 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management36 Questions
Exam 5: Advanced Linear Programming Applications30 Questions
Exam 6: Distribution and Network Models55 Questions
Exam 7: Integer Linear Programming41 Questions
Exam 8: Nonlinear Optimization Models44 Questions
Exam 9: Project Scheduling: Pertcpm47 Questions
Exam 10: Inventory Models43 Questions
Exam 11: Waiting Line Models40 Questions
Exam 12: Simulation43 Questions
Exam 13: Decision Analysis36 Questions
Exam 14: Multicriteria Decisions39 Questions
Exam 15: Forecasting38 Questions
Exam 16: Markov Processes31 Questions
Select questions type
When the cost of a resource is sunk, then the dual price can be interpreted as the
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
B
Relevant costs should be reflected in the objective function, but sunk costs should not.
Free
(True/False)
4.8/5  (29)
(29)
Correct Answer:
True
A section of output from The Management Scientist is shown here. 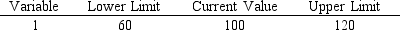 What will happen to the solution if the objective function coefficient for variable 1 decreases by 20?
What will happen to the solution if the objective function coefficient for variable 1 decreases by 20?
(Multiple Choice)
4.9/5  (32)
(32)
If the range of feasibility for b1 is between 16 and 37, then if b1 = 22 the optimal solution will not change from the original optimal solution.
(True/False)
4.9/5  (43)
(43)
To solve a linear programming problem with thousands of variables and constraints
(Multiple Choice)
4.8/5  (32)
(32)
A negative dual price for a constraint in a minimization problem means
(Multiple Choice)
4.9/5  (37)
(37)
Which of the following is not a question answered by sensitivity analysis?
(Multiple Choice)
4.9/5  (40)
(40)
A section of output from The Management Scientist is shown here. 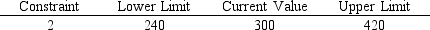 What will happen if the right-hand-side for constraint 2 increases by 200?
What will happen if the right-hand-side for constraint 2 increases by 200?
(Multiple Choice)
4.8/5  (31)
(31)
If the optimal value of a decision variable is zero and its reduced cost is zero, this indicates that alternative optimal solutions exist.
(True/False)
4.8/5  (40)
(40)
The dual price measures, per unit increase in the right hand side of the constraint,
(Multiple Choice)
4.8/5  (36)
(36)
Decreasing the objective function coefficient of a variable to its lower limit will create a revised problem that is unbounded.
(True/False)
4.8/5  (32)
(32)
Classical sensitivity analysis provides no information about changes resulting from a change in the coefficient of a variable in a constraint.
(True/False)
4.8/5  (36)
(36)
The amount by which an objective function coefficient can change before a different set of values for the decision variables becomes optimal is the
(Multiple Choice)
4.9/5  (37)
(37)
The dual value on the nonnegativitiy constraint for a variable is that variable's
(Multiple Choice)
4.8/5  (42)
(42)
If the dual price for the right-hand side of a constraint is zero, there is no upper limit on its range of feasibility.
(True/False)
4.8/5  (29)
(29)
Eight of the entries have been deleted from the LINDO output that follows. Use what you know about linear programming to find values for the blanks.
MIN 6 X1 + 7.5 X2 + 10 X3
SUBJECT TO
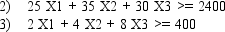 END
LP OPTIMUM FOUND AT STEP 2
OBJECTIVE FUNCTION VALUE
1) 612.50000
END
LP OPTIMUM FOUND AT STEP 2
OBJECTIVE FUNCTION VALUE
1) 612.50000
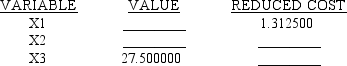
 NO. ITERATIONS= 2
RANGES IN WHICH THE BASIS IS UNCHANGED:
NO. ITERATIONS= 2
RANGES IN WHICH THE BASIS IS UNCHANGED:


(Essay)
4.8/5  (35)
(35)
If the range of feasibility indicates that the original amount of a resource, which was 20, can increase by 5, then the amount of the resource can increase to 25.
(True/False)
4.9/5  (34)
(34)
Showing 1 - 20 of 36
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)