Exam 7: Linear Systems
Exam 1: A Review of Basic Algebra149 Questions
Exam 2: Equations and Inequalities100 Questions
Exam 3: The Rectangular Coordinate System and Graphs of Equations75 Questions
Exam 4: Functions Functions and Function Notation75 Questions
Exam 5: Exponential and Logarithmic Functions75 Questions
Exam 6: Solving Polynomial Equations50 Questions
Exam 7: Linear Systems50 Questions
Exam 8: Conic Sections and Quadratic Systems75 Questions
Exam 9: Natural Number Functions and Probability297 Questions
Select questions type
Solve the system using Gaussian elimination. If is the solution to the system, give the value of .
(Multiple Choice)
4.7/5  (32)
(32)
Use Cramer's rule to find the solution of the system, if possible.
(Multiple Choice)
4.7/5  (35)
(35)
Find values of x and y, if any, that will make the matrices equal.
(Multiple Choice)
4.7/5  (42)
(42)
Solve the system by the addition method, if possible. If a solution exists, give the value of x.
(Multiple Choice)
5.0/5  (38)
(38)
Illustration shows three circles traced out by a figure skater during her performance.If the centers of the circles are the given distances apart, find the radius of each circle. 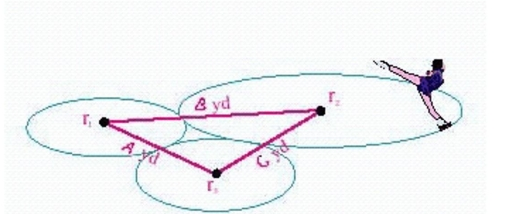
(Multiple Choice)
4.7/5  (46)
(46)
A diet requires at least 26 units of vitamin C and at least 31 units of vitamin B complex.Two food supplements are available that provide these nutrients, in the amounts and costs shown in the table
Below.How much of each should be used to minimize the cost? 
(Multiple Choice)
4.8/5  (41)
(41)
Two artists make winter yard ornaments. They get for each wooden snowman they make and for each wooden Santa Claus. On average, Nina must work 4 hours and Roberta 3 hours to make a snowman. Nina must work 2 hours and Roberta 4 hours to make a Santa Claus. If neither wishes to work more than 20 hours per week, how many of each ornament should they make each week to maximize their income? The information is summarized in the table below.
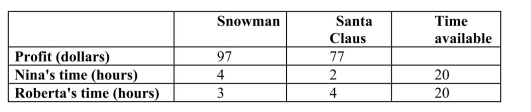
(Multiple Choice)
4.8/5  (30)
(30)
Solve the system by Gauss-Jordan elimination, if possible. If is the solution to the system, give the value of .
(Multiple Choice)
4.7/5  (35)
(35)
A diet requires at least 24 units of vitamin C and at least 26 units of vitamin B complex.Two food supplements are available that provide these nutrients, in the amounts and costs shown in the table
Below.How much of each should be used to minimize the cost? 
(Multiple Choice)
4.9/5  (36)
(36)
Showing 21 - 40 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)