Exam 4: Inverse, Exponential, and Logarithmic Functions
Exam 1: Topics From Algebra14 Questions
Exam 2: Functions and Graphs14 Questions
Exam 3: Polynomial and Rational Functions15 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions15 Questions
Exam 5: The Trigonometric Functions15 Questions
Exam 6: Analytic Trigonometry15 Questions
Exam 7: Applications of Trigonometry15 Questions
Exam 8: Systems of Equations and Inequalities15 Questions
Exam 9: Sequences, Series, and Probability15 Questions
Exam 10: Topics From Analytic Geometry15 Questions
Exam 11: Limits of Functions15 Questions
Select questions type
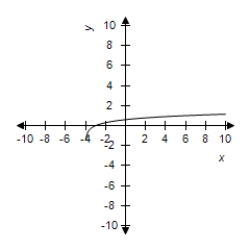
Use a graphing utility to graph the functions given by
and
in the same viewing window.
Free
(Short Answer)
4.7/5  (42)
(42)
Correct Answer:
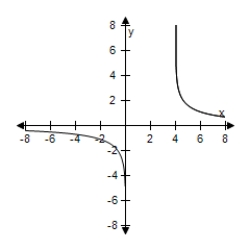
Determine whether the function has an inverse function. If it does, find the inverse function.
(Short Answer)
4.8/5  (36)
(36)
Approximate the point of intersection of the graphs of f and g. Then solve the equation algebraically to verify your approximation.
f(x)= g(x)=9 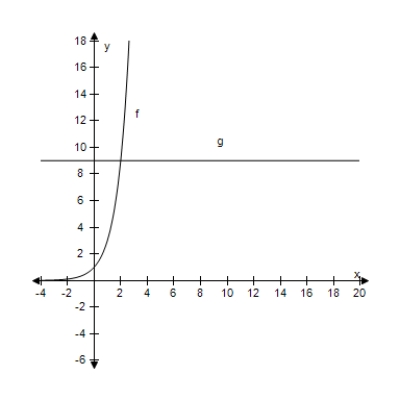
(Short Answer)
4.8/5  (34)
(34)
Use the change-of-base formula to rewrite the logarithm as a ratio of logarithms. Then use a
graphing utility to graph the ratio.
(Short Answer)
4.9/5  (34)
(34)
Use a graphing utility to construct a table of values for the function. Round your answer to two decimal places.
(Short Answer)
4.9/5  (43)
(43)
Evaluate the function at the indicated value of x. Round your result to three decimal places.
Function
Value
(Short Answer)
4.8/5  (30)
(30)
Your wage is $11.00 per hour plus $1.25 for each unit produced per hour. So, your hourly wage in terms of the number of units produced x is . Find the inverse function. What does each variable represent in the inverse function?
(Short Answer)
4.8/5  (36)
(36)
Use a graphing utility to construct a table of values for the function. Round your answer to three decimal places.
(Short Answer)
4.7/5  (34)
(34)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)