Exam 5: Analytic Trigonometry
Exam 1: Functions and Their Graphs121 Questions
Exam 2: Polynomial and Rational Functions129 Questions
Exam 3: Exponential and Logarithmic Functions46 Questions
Exam 4: Trigonometry61 Questions
Exam 5: Analytic Trigonometry67 Questions
Exam 6: Topics in Analytic Geometry100 Questions
Select questions type
Use the given values to evaluate (if possible) three trigonometric functions
(Multiple Choice)
4.8/5  (48)
(48)
Use the trigonometric substitution to select the algebraic expression as a trigonomet-
(Multiple Choice)
4.8/5  (39)
(39)
Use the figure to find the exact value of the trigonometric function. 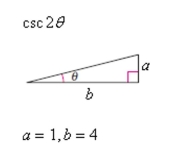
(Multiple Choice)
4.9/5  (35)
(35)
Use the sum-to-product formulas to select the sum or difference as a product.
(Multiple Choice)
4.8/5  (31)
(31)
Use the law of Cosines to solve the given triangle. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
Use inverse functions where needed to find all solutions (if they exist) of the given equation on the interval
(Multiple Choice)
4.7/5  (33)
(33)
Use the trigonometric substitution to select the algebraic expression as a trigonometric function of
(Multiple Choice)
4.8/5  (35)
(35)
Use the half-angle formulas to determine the exact value of the given trigonometric expression.
(Multiple Choice)
5.0/5  (34)
(34)
The table shows the average daily high temperatures in Houston H (in degrees Fahr- enheit) for month t, with corresponding to January. Month ,t Houston, H 1 62.4 2 66.4 3 73.4 4 79.4 5 85.4 6 90.4 7 93.4 8 93.5 9 89.4 10 82.4 11 72.4 12 64.4
Select the correct scatter plot from the above data.
(Multiple Choice)
4.8/5  (40)
(40)
Determine whether the Law of Sines or the Law of Cosines is needed to solve the tri- angle. Then solve the triangle.
(Multiple Choice)
4.8/5  (35)
(35)
Use the Heron's formula to find the area of the triangle. Round your answer upto two decimal places.
(Multiple Choice)
4.7/5  (38)
(38)
Use a graphing utility to select the correct graph in the same viewing window. Use the graphs to determine whether Explain your reasoning.
(Multiple Choice)
4.9/5  (32)
(32)
Determine whether the Law of Sines or the Law of Cosines is needed to solve the tri- angle. Then solve the triangle.
(Multiple Choice)
4.7/5  (33)
(33)
Given , use the Law of Cosines to solve the triangle for the value of C. Round answer to two decimal places. 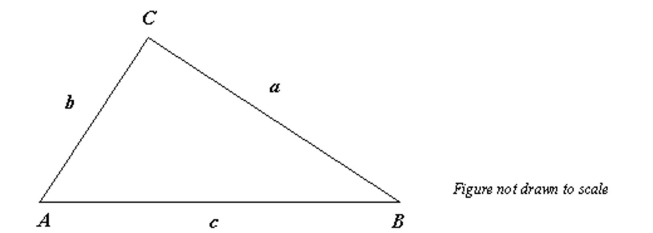
(Multiple Choice)
4.9/5  (31)
(31)
Determine the angle in the design of the streetlight shown in the following figure.
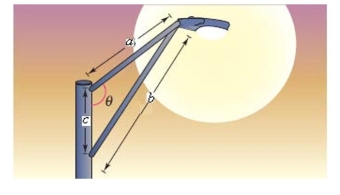
(Multiple Choice)
5.0/5  (41)
(41)
Showing 41 - 60 of 67
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)