Exam 1: Introduction
Exam 1: Introduction10 Questions
Exam 2: Forces, Moments, Resultants10 Questions
Exam 3: Equilibrium of Particles and Rigid Bodies: 2D, 3D11 Questions
Exam 4: Structural Applications10 Questions
Exam 5: Centroids, Center of Mass, Moments of Inertia9 Questions
Exam 6: Internal Effects in Bars, Shafts, Beams and Frames10 Questions
Exam 7: Tension, Compression and Shear12 Questions
Exam 8: Axially Loaded Members16 Questions
Exam 9: Torsion15 Questions
Exam 10: Stresses in Beams15 Questions
Exam 11: Analysis of Stress and Strain4 Questions
Exam 12: Applications of Plane Stress Pressure Vessels and Combined Loadings15 Questions
Select questions type
Vector ). The scalar product of these two vectors is:
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
A
Force (see figure) is applied at C and is directed toward A. Its magnitude is unit vector along line CA is:
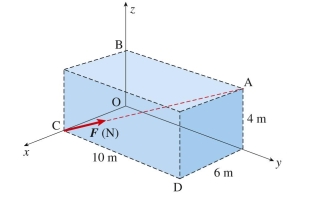
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
A
Vector ). The component of perpendicular to the line of action of vector is:
(Multiple Choice)
4.9/5  (37)
(37)
sum of orthogonal vectors . A unit vector along is Vector is:
(Multiple Choice)
4.9/5  (37)
(37)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)