Exam 8: Axially Loaded Members
Exam 1: Introduction10 Questions
Exam 2: Forces, Moments, Resultants10 Questions
Exam 3: Equilibrium of Particles and Rigid Bodies: 2D, 3D11 Questions
Exam 4: Structural Applications10 Questions
Exam 5: Centroids, Center of Mass, Moments of Inertia9 Questions
Exam 6: Internal Effects in Bars, Shafts, Beams and Frames10 Questions
Exam 7: Tension, Compression and Shear12 Questions
Exam 8: Axially Loaded Members16 Questions
Exam 9: Torsion15 Questions
Exam 10: Stresses in Beams15 Questions
Exam 11: Analysis of Stress and Strain4 Questions
Exam 12: Applications of Plane Stress Pressure Vessels and Combined Loadings15 Questions
Select questions type
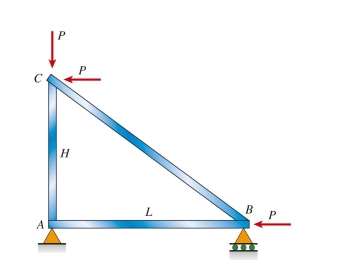
A steel plane truss is loaded at B and C by forces P =200 kN. The cross-sectional area of each member . Truss dimensions are H=3 m and L = 4 m. The maximum shear stress in bar AB is approx- imately:
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
C
walls by a nut and washer assembly at each end. If the allowable bearing stress between the washer and wall is and the allowable normal stress in the rod is , the maximum permissible temperature drop is approximately:

Free
(Multiple Choice)
4.9/5  (42)
(42)
Correct Answer:
A
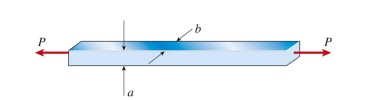
A steel bar of rectangular cross section (a = 38 mm, b = 50 mm) carries a tensile load P. The allowable stresses in tension and shear are 100 MPa and 48 MPa, respectively. The maximum permissible load is Approximately:
Free
(Multiple Choice)
4.9/5  (47)
(47)
Correct Answer:
D
A copper bar (d = 10 mm, E = 110 GPa) is loaded by tensile load P = 11.5 kN. The maximum shear stress in the bar is approximately:

(Multiple Choice)
4.9/5  (34)
(34)
nylon bar (E = 2.1 GPa) with diameter 12 mm, length 4.5 m, and weight 5.6 N hangs vertically under its own weight. The elongation of the bar at its free end is approximately: 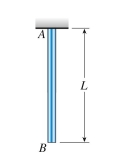
(Multiple Choice)
4.7/5  (34)
(34)
brass bar (E = 110 MPa) of length mm over one-half of its length and mm over the other half. Compare this nonprismatic bar to a prismatic bar of the same volume of material with constant diameter d and length L. The elongation of the prismatic bar under the same load P = 25 kN is approximately: 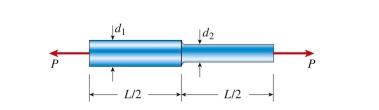
(Multiple Choice)
4.8/5  (43)
(43)
wires, one copper and the other steel, of equal length stretch the same amount under an applied load P. The moduli of elasticity for each is GPa. The ratio of the diameter of the copper Wire to that of the steel wire is approximately: 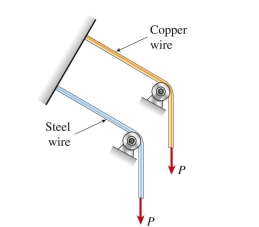
(Multiple Choice)
4.8/5  (42)
(42)
A steel bolt is enclosed by a copper tube (length = 0.5 m, area = and the end nut is turned until it is just snug. The pitch of the bolt threads is 1.25 mm. The bolt is now tightened by a quarter turn of the nut. The resulting stress in the bolt is approximately:
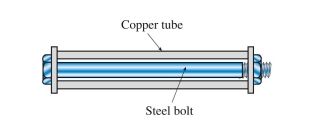
(Multiple Choice)
4.8/5  (42)
(42)
clevis and pin assembly at each end. If the allowable shear stress in the pin is and the allowable normal stress in the rod is , the maximum permissible temperature drop is approximately:
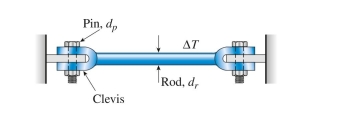
(Multiple Choice)
4.9/5  (36)
(36)
Initially, both shell and core have a length of 100 mm. A load P is applied to both shell and core through a cap plate. The load P required to compress both shell and core by 0.10 mm is approximately: 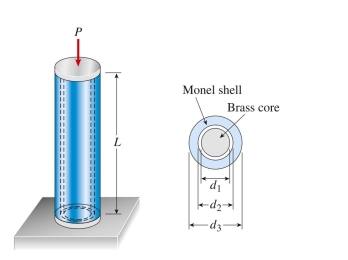
(Multiple Choice)
4.7/5  (40)
(40)
, and . Segment lengths of the bar are , and . The change in length of the bar is approximately: 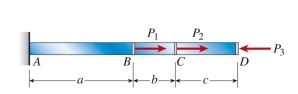
(Multiple Choice)
4.8/5  (32)
(32)
plane truss with span length L = 4.5 m is constructed using cast iron pipes with a cross-sectional area of The displacement of joint B cannot exceed 2.7 mm. The maximum value of
Loads P is approximately: 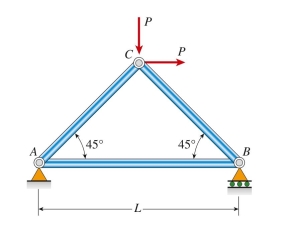
(Multiple Choice)
4.8/5  (37)
(37)
nonprismatic cantilever bar has an internal cylindrical hole of diameter from 0 to x, so the net area of the cross section for Segment 1 is applied at x 5 L. Assume That E is constant. The length of the hollow segment, x, required to obtain axial displacement δ 5 PL/EA at the Free end is:
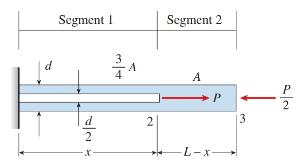
(Multiple Choice)
4.8/5  (32)
(32)
A brass wire (d = 2.0 mm, E = 110 GPa) is pretensioned to T = 85 N. The coefficient of thermal expan- sion for the wire is . The temperature change at which the wire goes slack is approximately:

(Multiple Choice)
4.8/5  (35)
(35)
A plane stress element on a bar in uniaxial stress has a tensile stress of (see figure). The maximum shear stress in the bar is approximately:
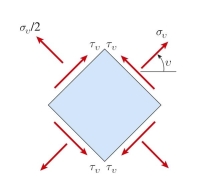
(Multiple Choice)
4.7/5  (37)
(37)
A prismatic bar (diameter with radius of fillets ) is loaded by force . The allowable axial stress in the material is . The ratio of the maximum permissible loads that can be applied to the bars, considering stress concentration effects in the stepped bar, is: 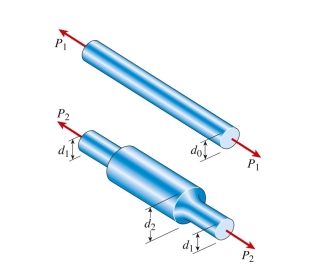
(Multiple Choice)
4.9/5  (40)
(40)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)