Exam 2: Limits and the Derivative
Exam 1: Functions and Graphs224 Questions
Exam 2: Limits and the Derivative123 Questions
Exam 3: Additional Derivative Topics126 Questions
Exam 4: Graphing and Optimization116 Questions
Exam 5: Integration93 Questions
Exam 6: Additional Integration Topics82 Questions
Exam 7: Multivariable Calculus78 Questions
Exam 8: Trigonometric Functions92 Questions
Exam 9: Differential Equations47 Questions
Exam 10: Taylor Polynomials and Infinite Series48 Questions
Exam 11: Probability and Calculus57 Questions
Exam 12: Basic Algebra Review44 Questions
Exam 13: Special Topics20 Questions
Select questions type
Provide an appropriate response.
-The revenue (in thousands of dollars) from producing x units of an item is modeled R 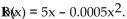 Find the marginal revenue at x = 1000.
Find the marginal revenue at x = 1000.
(Multiple Choice)
4.9/5  (34)
(34)
Find the limit, if it exists.
-Evaluate the following limit. 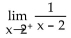
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-A company training program determines that, on average, a new employee can do P(x) pieces of work per day after s days of on-the-job training, where 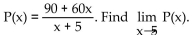
(Multiple Choice)
5.0/5  (32)
(32)
Provide an appropriate response.
-Let C(x) be the cost function and R(x) the revenue function. Compute the marginal cost, marginal revenue, and the marginal profit functions. 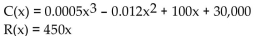
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-Suppose an object moves along the y-axis so that its location is 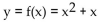 at time x (y is in meters and x is in seconds). Find the average velocity (the average rate of change of y with respect to x) for x changing from 2 to
9 seconds.
at time x (y is in meters and x is in seconds). Find the average velocity (the average rate of change of y with respect to x) for x changing from 2 to
9 seconds.
(Multiple Choice)
4.7/5  (42)
(42)
Provide an appropriate response.
-The total cost to produce x units of paint is C(x) = (5x + 3)(7x + 4). Find the marginal average cost function.
(Multiple Choice)
4.9/5  (34)
(34)
Sketch a possible graph of a function that satisfies the given conditions.
-f(1) = 4; 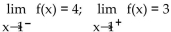
(Multiple Choice)
4.7/5  (32)
(32)
Provide an appropriate response.
-Use a graphing utility to find the discontinuities of the given rational function. 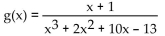
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-If an object moves along a line so that it is at 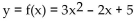 at time x (in seconds), find the instantaneous velocity function
at time x (in seconds), find the instantaneous velocity function 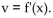
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-A cube 4 inches on an edge is given a protective coating 0.2 inches thick. About how much coating should a production manager order for 800 cubes?
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Suppose an object moves along the y-axis so that its location is 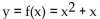 at time x (y is in meters and x is in seconds). Find the instantaneous velocity at x = 4 seconds.
at time x (y is in meters and x is in seconds). Find the instantaneous velocity at x = 4 seconds.
(Multiple Choice)
4.7/5  (30)
(30)
Solve the problem.
-The demand equation for a certain item is 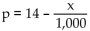 and the cost equation is C(x) = 7,000 + 4x. Find the marginal profit at a production level of 3,000 and interpret the result.
and the cost equation is C(x) = 7,000 + 4x. Find the marginal profit at a production level of 3,000 and interpret the result.
(Multiple Choice)
4.9/5  (43)
(43)
Solve the problem.
-Suppose that the cost C of removing p% of the pollutants from a chemical dumping site is given by 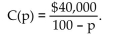 Can a company afford to remove 100% of the pollutants? Explain.
Can a company afford to remove 100% of the pollutants? Explain.
(Multiple Choice)
4.9/5  (40)
(40)
Sketch a possible graph of a function that satisfies the given conditions.
-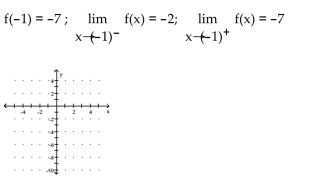
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-Suppose that the value V of a certain product decreases, or depreciates, with time t, in months, where 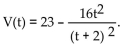
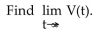
(Multiple Choice)
4.8/5  (42)
(42)
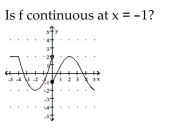
The graph of y = f(x) is shown. Use the graph to answer the question.
-
(Multiple Choice)
4.7/5  (34)
(34)
Showing 101 - 120 of 123
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)