Exam 9: Sequences; Induction; the Binomial Theorem
Exam 1: Equations and Inequalities365 Questions
Exam 2: Graphs83 Questions
Exam 3: Functions and Their Graphs112 Questions
Exam 4: Linear and Quadratic Functions21 Questions
Exam 5: Polynomial and Rational Functions45 Questions
Exam 6: Exponential and Logarithmic Functions234 Questions
Exam 7: Analytic Geometry129 Questions
Exam 8: Systems of Equations and Inequalities428 Questions
Exam 9: Sequences; Induction; the Binomial Theorem242 Questions
Exam 10: Counting and Probability110 Questions
Exam 11: Graphing Utilities25 Questions
Select questions type
Find the indicated term of the geometric sequence.
-6th term of -1, 3, -9, ...
Free
(Multiple Choice)
4.8/5  (43)
(43)
Correct Answer:
A
Mathematical Induction
1 Prove Statements Using Mathematical Induction
Write the word or phrase that best completes each statement or answers the question.
Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.
-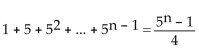
Free
(Essay)
4.9/5  (30)
(30)
Correct Answer:
First, we show that the statement is true when n = 1.
For n = 1, we get 1 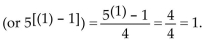 This is a true statement and Condition I is satisfied.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is, 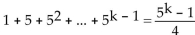 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that 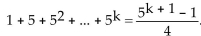 So we assume that 1
So we assume that 1 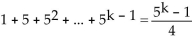 is true and add the next term,
is true and add the next term, 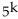 to both sides of the equation.
to both sides of the equation. 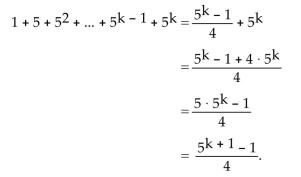 Condition II is satisfied. As a result, the statement is true for all natural numbers n.
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
Find the indicated term using the given information.
--1 , 2 , 5 , ... ; 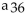
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
A
Use a graphing utility to find the sum of the geometric sequence. Round answer to two decimal places, if necessary.
-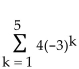
(Multiple Choice)
4.8/5  (37)
(37)
A geometric sequence is given. Find the common ratio and write out the first four terms.
-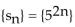
(Multiple Choice)
4.8/5  (31)
(31)
Mathematical Induction
1 Prove Statements Using Mathematical Induction
Write the word or phrase that best completes each statement or answers the question.
Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.
-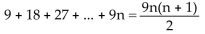
(Essay)
4.9/5  (31)
(31)
Use the Binomial Theorem to find the indicated coefficient or term.
-The 5th term in the expansion of ( 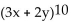
(Multiple Choice)
4.7/5  (43)
(43)
Use a graphing utility to find the sum of the geometric sequence. Round answer to two decimal places, if necessary.
-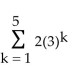
(Multiple Choice)
4.8/5  (29)
(29)
The sequence is defined recursively. Write the first four terms.
-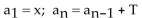
(Multiple Choice)
4.9/5  (36)
(36)
Use a graphing utility to find the sum of the geometric sequence. Round answer to two decimal places, if necessary.
-4 + 12 + 36 + 108 + 324 + ... + 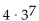
(Multiple Choice)
4.7/5  (47)
(47)
Determine whether the given sequence is arithmetic, geometric, or neither. If the sequence is arithmetic, find the
common difference; if it is geometric, find the common ratio.
-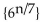
(Multiple Choice)
4.7/5  (37)
(37)
Solve.
-After working for 25 years you would like to have $800,000 in an annuity for early retirement. If theannual interest rate is 7.5%, compounded monthly, what will your monthly deposit need to be?
(Multiple Choice)
4.9/5  (37)
(37)
Showing 1 - 20 of 242
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)