Exam 6: Reducing Rational Expressions to Lowest Terms
Exam 1: Notation and Symbols329 Questions
Exam 2: Simplifying Expressions285 Questions
Exam 3: Paired Data and Graphing Ordered Pairs217 Questions
Exam 4: Multiplication With Exponents300 Questions
Exam 5: The Greatest Common Factor and Factoring by Grouping295 Questions
Exam 6: Reducing Rational Expressions to Lowest Terms263 Questions
Exam 7: Review of Solving Equations262 Questions
Exam 8: The Slope of a Line190 Questions
Exam 9: Rational Exponents264 Questions
Exam 10: Completing the Square187 Questions
Exam 11: Exponential Functions226 Questions
Exam 12: The Circle95 Questions
Exam 13: Sequences190 Questions
Select questions type
One car travels 180 miles in the same amount of time it takes a second car traveling 6 miles per hour slower than the first to go 162 miles. What are the speeds of the cars?
(Multiple Choice)
4.9/5  (34)
(34)
Solve the following equation. Be sure to check each answer in the original equation if you multiply both sides by an expression that contains the variable. 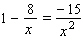
(Multiple Choice)
4.8/5  (35)
(35)
Reduce the following rational expression to lowest terms, if possible. 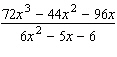
(Multiple Choice)
4.7/5  (28)
(28)
Graph 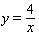 and
and 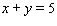 on the same coordinate system. At what points do the two graphs intersect?
on the same coordinate system. At what points do the two graphs intersect?
(Multiple Choice)
4.7/5  (40)
(40)
Solve the following equation. Be sure to check each answer in the original equation if you multiply both sides by an expression that contains the variable. 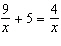
(Multiple Choice)
4.9/5  (32)
(32)
The following problem involves some factoring by grouping. Remember, before you can divide out factors common to the numerator and denominator of a product, you must factor completely. 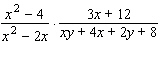
(Multiple Choice)
4.8/5  (30)
(30)
Reduce the following rational expression to lowest terms, if possible. 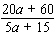
(Multiple Choice)
4.8/5  (27)
(27)
One plane can travel 10 miles per hour faster than another. One of them goes 400 miles in the same time it takes the other to go 375 miles. What are their speeds? _____ , _____ miles per hour
(Short Answer)
4.8/5  (33)
(33)
A solution contains 15 milliliters of alcohol and 20 milliliters of water. If another solution is to have the same concentration of alcohol in water but is to contain 32 milliliters of water, how much alcohol must it contain? __________ milliliters
(Short Answer)
4.8/5  (38)
(38)
Showing 101 - 120 of 263
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)