Chat with AIExam 7: Linear Regression
Define regression line.
(45) 
Answered by Examlex AI CopilotA regression line, also known as a line of best fit, is a straight line that best represents the data on a scatter plot. This line is used in regression analysis, which is a statistical method for modeling the relationship between a dependent variable and one or more independent variables.
The purpose of the regression line is to predict the value of the dependent variable based on the values of the independent variable(s). The line is calculated using the least squares method, which minimizes the sum of the squares of the vertical distances (residuals) between the observed values and the values predicted by the line.
In the simplest form of regression analysis, linear regression, the regression line has the equation:
Y = a + bX + ε
where:
- Y is the dependent variable,
- X is the independent variable,
- a is the y-intercept (the value of Y when X = 0),
- b is the slope of the line (the change in Y for a one-unit change in X),
- ε is the error term (the difference between the observed values and the values predicted by the line).
The coefficients a and b are determined during the regression analysis such that they provide the best fit for the data points. The goodness of fit of the regression line is often evaluated using the coefficient of determination (R²), which measures the proportion of the variance in the dependent variable that is predictable from the independent variable(s).
In summary, a regression line is a statistical tool that represents the relationship between variables and is used to predict outcomes. It is a foundational concept in many fields that require data analysis, including economics, biology, engineering, and social sciences.
In a particular relationship N = 80. How many points would you expect on the average to find within 1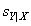 
of the regression line?
of the regression line? (44) 
VerifiedC
Why is it important to know the standard error of estimate for a set of paired scores?
(36) Answered by Examlex AI CopilotThe standard error of the estimate (SEE) is a measure of the accuracy of predictions made with a regression line. It is important to know the standard error of estimate for a set of paired scores because it provides valuable information about the quality of the regression model and the reliability of the predictions made from it. Here are several reasons why SEE is important:
1. **Measure of Prediction Accuracy**: The standard error of the estimate quantifies how much the actual data points deviate from the predicted values based on the regression line. A smaller SEE indicates that the data points are closer to the regression line, which means the predictions are more accurate.
2. **Model Evaluation**: SEE is used to evaluate the performance of a regression model. By comparing the standard errors of different models, you can determine which model has a better fit for the data.
3. **Confidence in Results**: Knowing the SEE helps in assessing the confidence you can have in the regression model's predictions. It allows you to estimate the range within which the true value of the dependent variable lies for a given value of the independent variable.
4. **Comparison of Variables**: When standardizing the variables, the SEE can be used to compare the predictive power of different independent variables within the same regression model or across different models.
5. **Hypothesis Testing**: In statistical hypothesis testing, the SEE is used to calculate the t-statistic for assessing the significance of individual predictors in the model. This helps in understanding which variables have a meaningful impact on the dependent variable.
6. **Assumption Checking**: The SEE can be used to check the assumptions of the regression analysis, such as homoscedasticity (constant variance of the errors). If the SEE is not consistent across different values of the independent variable, it may indicate that the assumption of homoscedasticity is violated.
7. **Scaling of Data**: The SEE is not affected by the scaling of the data, which means it is a dimensionless measure. This allows for the comparison of the quality of regression models across different datasets or studies.
In summary, the standard error of the estimate is a crucial statistic in regression analysis because it provides insight into the precision and reliability of the model's predictions. It is a key component in determining the goodness of fit of the model, comparing different models, and conducting hypothesis tests on the model's parameters.
Consider the following set of data points: 
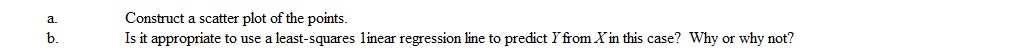
For regression purposes, it is customary to assign X to the variable we are predicting from.
(40) It is impossible to have a negative value for the standard error of estimate.
(37) When doing regression, it is customary to assign X to the predicted variable .
(34) For the following points what would you predict to be the value of Y' when X = 19? Assume a linear relationship. 
(28) If the relationship between two variables is perfect the standard error of estimate equals 0.
(48) X represents aptitude test scores and Y represents grade point average in college. If the least-squares regression line for the relationship between these two variables is Y' = .005 X + 1.2, what GPA would you predict for people who scored each of the following scores on the aptitude test?
A researcher collects data on the relationship between the amount of daily exercise an individual gets and the percent body fat of the individual. The following scores are recorded. 
Assuming a linear relationship holds, the least squares regression line for predicting % fat from the amount of exercise an individual gets is _________.
Assuming a linear relationship holds, the least squares regression line for predicting % fat from the amount of exercise an individual gets is _________. (38) To do linear regression, there must be paired scores on two variables.
(41) If we minimize Σ( Y - Y' ) 2 , we will minimize the total error of prediction.
(31) When doing regression, what is the convention used for assigning X and Y to the data?
(35) When the relationship is perfect, the regression of Y on X is the same as the regression of X on Y.
(25) If the value of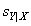 
= 4.00 for relationship A and 
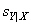= 5.25 for relationship B , in which relationship would you have the most confidence in a particular prediction?
= 4.00 for relationship A and = 5.25 for relationship B , in which relationship would you have the most confidence in a particular prediction? (28) If the correlation between two sets of scores is 0 and one had to predict the value of Y for any given value of X , the best prediction of Y would be _________.
(38) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)