Exam 4: Systems of Equations and Inequalities
Exam 1: Fundamentals of Algebra149 Questions
Exam 2: Linear Equations and Inequalities121 Questions
Exam 3: Graphs and Functions162 Questions
Exam 4: Systems of Equations and Inequalities101 Questions
Exam 5: Polynomials and Factoring158 Questions
Exam 6: Rational Expressions, Equations, and Functions143 Questions
Exam 7: Radicals and Complex Numbers130 Questions
Exam 8: Quadratic Equations, Functions, and Inequalities122 Questions
Exam 9: Exponential and Logarithmic Functions165 Questions
Exam 10: Conics89 Questions
Exam 11: Sequences, Series, and the Binomial Theorem98 Questions
Select questions type
The sum of three positive numbers is . The second number is 5 than the first, and the third is 5 times the first. What is the number?
(Multiple Choice)
4.8/5  (45)
(45)
Solve the system of linear equations below by the method of elimination, if a single solution exists.
(Multiple Choice)
4.7/5  (28)
(28)
Solve the system of linear equations below by the method of elimination, if a single solution exists.
(Multiple Choice)
4.7/5  (36)
(36)
Describe the elementary row operation used to transform the first matrix into the second matrix .
(Multiple Choice)
4.8/5  (38)
(38)
Solve for x in the matrix below by using elementary row operations to form a row-equivalent matrix.
(Multiple Choice)
4.9/5  (35)
(35)
Determine the value of k such that the system of linear equations below is inconsistent.
(Multiple Choice)
4.7/5  (39)
(39)
Solve the system of equations below by the method of substitution.
(Multiple Choice)
4.8/5  (29)
(29)
A person plans to invest up to $10,000 in two different interest-bearing accounts, account X and account Y. Account Y is to contain at least $ . Moreover, account X should have at least twice the amount in account Y. Graph the system of linear inequalities describing the various amounts that can be deposited in each account.
(Multiple Choice)
5.0/5  (38)
(38)
Use matrices to solve the system of linear equations below.
(Multiple Choice)
4.8/5  (35)
(35)
Determine whether the system is consistent or inconsistent.
(Multiple Choice)
4.9/5  (39)
(39)
Use the graph of the equation to determine whether the system has any solutions. Find any solutions that exist. 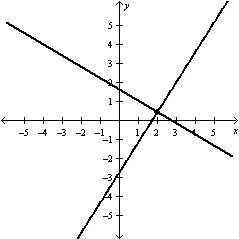
(Multiple Choice)
4.8/5  (44)
(44)
Evaluate the determinant of the matrix. Expand by minors along the row or column that appears to make the computation easiest.
(Multiple Choice)
4.9/5  (43)
(43)
Solve the system of linear equations below by the method of elimination.
(Multiple Choice)
4.9/5  (40)
(40)
A total of is invested in two bonds that pay and simple interest. The annual interest is . How much is invested in the bond?
(Multiple Choice)
4.9/5  (39)
(39)
Find two positive integers that satisfy the requirements that the difference of four times the smaller number and the larger number is 14 and the sum of the smaller number and four times the larger number is 335 .
(Multiple Choice)
4.7/5  (43)
(43)
A grocer wishes to mix three kinds of nuts to obtain pounds of a mixture priced at per pound. Peanuts cost per pound, almonds cost per pound, and pistachios cost per pound. Half of the mixture is composed of peanuts and almonds. How many pounds of should the grocer use?
(Multiple Choice)
4.8/5  (36)
(36)
Form the coefficient matrix for the system of linear equations below.
(Multiple Choice)
5.0/5  (40)
(40)
Showing 61 - 80 of 101
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)