Note: the solutions to most of the multiple choice questions in these sections use what call the standard assignment of truth values to atomic propositions. The standard assignment of truth values assigns the values given here to the variables in the wffs in the exercises, when read left to right. So, the first variable in the formula read left to right gets the α assignment; the second variable in the formula read left to right (if any) gets the β assignment; the third variable in the formula read left to right (if any) gets the γ assignment; and the fourth variable in the formula read left to right (if any) gets the δ assignment. For exercises with only one propositional variable, the standard assignment is: $\begin{array} { |l| } \hline \alpha\\ \hline \text { 1}\\ \hline \text {0 }\\\hline \end{array}$ For exercises with two propositional variables, the standard assignment is: \[\begin{array} { | c | c | } \hline \alpha& \boldsymbol { \beta } \\ \hline 1 & 1 \\ \hline 1 & 0 \\ \hline 0 & 1 \\ \hline0& 0\\ \hline \end{array}\] For exercises with three propositional variables, the standard assignment is: \[\begin{array} { | c | c | c | } \hline \alpha & \beta & \gamma \\ \hline 1 & 1 & 1 \\ \hline 1 & 1 & 0 \\ \hline 1 & 0 & 1 \\ \hline 1 & 0& 0e \\ \hline 0 & 1 & 1 \\ \hline 0 & 1 & 0 \\ \hline 0 &0& 1 \\ \hline 0 & 0& 0 \\ \hline \end{array}\] For exercises with four propositional variables, the standard assignment is: \[\begin{array} { | l | l | l | l | } \hline \alpha & \boldsymbol { \beta } &\gamma& \delta\ \\ \hline 1 & 1 & 1 & 1 \\ \hline 1 & 1 & 1 & 0 \\ \hline 1 & 1 & 0 & 1 \\ \hline 1 & 1 & 0 & 0 \\ \hline 1 & 0 & 1 & 1 \\ \hline 1 & 0 & 1 & 0\\ \hline 1 & 0 & 0 & 1 \\ \hline 1 & 0& 0 & 0 \\ \hline 0 & 1 & 1 & 1 \\ \hline 0 & 1 & 1 &0 \\ \hline \end{array}\] \[\begin{array} { | c | c | c | c | } \hline 0 & 1 & 0 & 1 \\ \hline 0 & 1 & 0 & 0 \\ \hline 0& 0 & 1 & 1 \\ \hline 0 & 0 & 1 & 0 \\ \hline 0 & 0 & 0 & 1 \\ \hline 0 & 0 & 0 & 0 \\ \hline \end{array}\] \[\begin{array} { |l | l | l | l |} \hline 0 & 1 & 0 & 1 \\ \hline \end{array}\] For each of the given propositions, determine which of the given sequences properly describes the column under the main operator, given the standard assignment of truth values to atomic propositions. -(I ? J) $ \lor $ (J ? I)

A) 1111 B) 1100 C) 1010 D) 0000 A) 1111 B) 1100 C) 1010 D) 0000

Note: the solutions to most of the multiple choice questions in these sections use what call the standard assignment of truth values to atomic propositions. The standard assignment of truth values assigns the values given here to the variables in the wffs in the exercises, when read left to right. So, the first variable in the formula read left to right gets the α assignment; the second variable in the formula read left to right (if any) gets the β assignment; the third variable in the formula read left to right (if any) gets the γ assignment; and the fourth variable in the formula read left to right (if any) gets the δ assignment. For exercises with only one propositional variable, the standard assignment is: $\begin{array} { |l| } \hline \alpha\\ \hline \text { 1}\\ \hline \text {0 }\\\hline \end{array}$ For exercises with two propositional variables, the standard assignment is: \[\begin{array} { | c | c | } \hline \alpha& \boldsymbol { \beta } \\ \hline 1 & 1 \\ \hline 1 & 0 \\ \hline 0 & 1 \\ \hline0& 0\\ \hline \end{array}\] For exercises with three propositional variables, the standard assignment is: \[\begin{array} { | c | c | c | } \hline \alpha & \beta & \gamma \\ \hline 1 & 1 & 1 \\ \hline 1 & 1 & 0 \\ \hline 1 & 0 & 1 \\ \hline 1 & 0& 0e \\ \hline 0 & 1 & 1 \\ \hline 0 & 1 & 0 \\ \hline 0 &0& 1 \\ \hline 0 & 0& 0 \\ \hline \end{array}\] For exercises with four propositional variables, the standard assignment is: \[\begin{array} { | l | l | l | l | } \hline \alpha & \boldsymbol { \beta } &\gamma& \delta\ \\ \hline 1 & 1 & 1 & 1 \\ \hline 1 & 1 & 1 & 0 \\ \hline 1 & 1 & 0 & 1 \\ \hline 1 & 1 & 0 & 0 \\ \hline 1 & 0 & 1 & 1 \\ \hline 1 & 0 & 1 & 0\\ \hline 1 & 0 & 0 & 1 \\ \hline 1 & 0& 0 & 0 \\ \hline 0 & 1 & 1 & 1 \\ \hline 0 & 1 & 1 &0 \\ \hline \end{array}\] \[\begin{array} { | c | c | c | c | } \hline 0 & 1 & 0 & 1 \\ \hline 0 & 1 & 0 & 0 \\ \hline 0& 0 & 1 & 1 \\ \hline 0 & 0 & 1 & 0 \\ \hline 0 & 0 & 0 & 1 \\ \hline 0 & 0 & 0 & 0 \\ \hline \end{array}\] \[\begin{array} { |l | l | l | l |} \hline 0 & 1 & 0 & 1 \\ \hline \end{array}\] For each of the given propositions, determine which of the given sequences properly describes the column under the main operator, given the standard assignment of truth values to atomic propositions. -(S ? ?T) ? {[V ? (?S • T)] $ \lor $ [V ? (?T • S)]}

A) 0011 1111 B) 0011 0000 C) 0101 1101 D) 1111 0101 E) 1111 1101 A) 0011 1111 B) 0011 0000 C) 0101 1101 D) 1111 0101 E) 1111 1101

Note: the solutions to most of the multiple choice questions in these sections use what call the standard assignment of truth values to atomic propositions. The standard assignment of truth values assigns the values given here to the variables in the wffs in the exercises, when read left to right. So, the first variable in the formula read left to right gets the α assignment; the second variable in the formula read left to right (if any) gets the β assignment; the third variable in the formula read left to right (if any) gets the γ assignment; and the fourth variable in the formula read left to right (if any) gets the δ assignment. For exercises with only one propositional variable, the standard assignment is: $\begin{array} {| l | } \hline \alpha\\\hline \text {1 }\\\hline \text {0 }\\\hline \end{array}$ For exercises with two propositional variables, the standard assignment is: \[\begin{array} { | c | c | } \hline \mathbf { n } & \boldsymbol { \beta } \\ \hline 1 & 1 \\ \hline 1 & 0 \\ \hline 0 & 1 \\ \hline 0 & 0 \\ \hline \end{array}\] For exercises with three propositional variables, the standard assignment is: \[\begin{array} { | c | c | c | } \hline \alpha & \beta & \gamma \\ \hline 1 & 1 & 1 \\ \hline 1 & 1 & 0 \\ \hline 1 & 0 & 1 \\ \hline 1 & 0 & 0 \\ \hline 0 & 1 & 1 \\ \hline 0 & 1 & 0 \\ \hline 0& 0 & 1 \\ \hline 0 & 0 &0\\ \hline \end{array}\] For exercises with four propositional variables, the standard assignment is: $\begin{array}{|c|c|c|c|} \hline\alpha & \beta & \gamma & \delta \\ \hline 1 & 1 & 1 & 1 \\ \hline 1 & 1 & 1 & 0 \\ \hline 1 & 1 & 0 & 1 \\ \hline 1 & 1 & 0 & 0\\ \hline 1 & 0 & 1 & 1 \\ \hline 1 & 0 & 1 & 0 \\ \hline 1 & 0 & 0 & 1 \\ \hline 1 & 0 & 0 & 0 \\ \hline 0 & 1 & 1 & 1 \\ \hline 0 & 1 & 1 & 0 \\ \hline 0 & 1 & 0 & 1\\ \hline 0 & 1 & 0 & 0 \\ \hline 0 & 0 & 1 & 1 \\ \hline 0 & 0 & 1 & 0 \\ \hline 0 & 0 & 0 & 1 \\ \hline 0 & 0 & 0 & 0\\\hline \end{array}$ Complete truth tables for each of the following propositions. -(S ⊃ ∼T) ⊃ {[V ⊃ (∼S ⊃ T)] $ \lor $ [V ⊃ (∼T ⊃ S)]}

The answer of Note: the solutions to most of the...

Exam 2: Propositional Logic: Syntax and Semantic

construct a complete truth table for each of the following pairs of propositions. Then, using the truth table, determine whether the statements are logically equivalent or contradictory. If neither, determine whether they are consistent or inconsistent. -G ≡ ∼H and (H • ∼G) $\lor$ (G • ∼H)

Free

(Multiple Choice)

4.9/5

(37)

Question 1

Correct Answer:

Verified

A

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, choose an option which presents a counterexample. (There may be other counterexamples as well.) -I ⊃ J ∼(J • I) / J ⊃ I

Free

(Multiple Choice)

4.8/5

(38)

Question 2

Correct Answer:

Verified

D

Instructions: For questions 11-20, construct complete a truth table for each of the following pairs of propositions. Then, using the truth table, determine whether the statements are logically equivalent or contradictory. If neither, determine whether they are consistent or inconsistent. Justify your answers. -P ⊃ [Q ⊃ (∼S ⊃ ∼R)] and ∼P $\lor$ ∼[(Q • ∼S) • R]

Free

(Essay)

4.9/5

(39)

Question 3

Correct Answer:

Verified

Logically equivalent

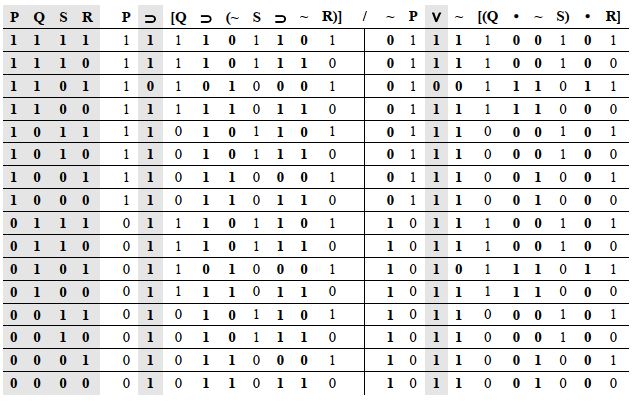
Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, choose an option which presents a counterexample. (There may be other counterexamples as well.) -B $\lor$ ∼C ∼∼C / ∼B

(Multiple Choice)

4.9/5

(47)

Question 4

Instructions: For questions 11-20, construct complete a truth table for each of the following pairs of propositions. Then, using the truth table, determine whether the statements are logically equivalent or contradictory. If neither, determine whether they are consistent or inconsistent. Justify your answers. -L $\lor$ (M ⊃ N) and ∼L • (M • ∼N)

(Essay)

4.8/5

(41)

Question 5

Note: the solutions to most of the multiple choice questions in these sections use what call the standard assignment of truth values to atomic propositions. The standard assignment of truth values assigns the values given here to the variables in the wffs in the exercises, when read left to right. So, the first variable in the formula read left to right gets the α assignment; the second variable in the formula read left to right (if any) gets the β assignment; the third variable in the formula read left to right (if any) gets the γ assignment; and the fourth variable in the formula read left to right (if any) gets the δ assignment. For exercises with only one propositional variable, the standard assignment is: \alpha 1 0 For exercises with two propositional variables, the standard assignment is: \alpha 1 1 1 0 0 1 0 0 For exercises with three propositional variables, the standard assignment is: \alpha \beta \gamma 1 1 1 1 1 0 1 0 1 1 0 0e 0 1 1 0 1 0 0 0 1 0 0 0 For exercises with four propositional variables, the standard assignment is: \alpha \gamma \delta\ 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 For each of the given propositions, determine which of the given sequences properly describes the column under the main operator, given the standard assignment of truth values to atomic propositions. -(I ? J) $\lor$ (J ? I)

(Multiple Choice)

4.8/5

(39)

Question 6

use indirect truth tables to determine whether each of the following arguments is valid. If the argument is invalid, specify a counterexample. -D ⊃ (E $\lor$ F) D ⊃ (G $\lor$ F) ∼(F $\lor$ H) / D ⊃ (E • G)

(Short Answer)

4.7/5

(43)

Question 7

Instructions: For questions 11-20, construct complete a truth table for each of the following pairs of propositions. Then, using the truth table, determine whether the statements are logically equivalent or contradictory. If neither, determine whether they are consistent or inconsistent. Justify your answers. -J ⊃ (K ⊃ ∼J) and J • K

(Essay)

4.9/5

(40)

Question 8

use the following key to translate each of the arguments of PL into natural, English arguments. A: Peirce studied logic. B: James was a pluralist. C: Dewey wrote about thirdness. D: Dewey denigrated the quest for certainty. E: Peirce emphasized education. -1. ∼C ⊃ (A ≡ B) 2. D $\lor$ ∼E 3. ∼D • (∼E ⊃ ∼C) / B ⊃ A

(Essay)

4.9/5

(42)

Question 9

use the following key to translate each of the given arguments into symbols of PL. B: Brouwer is an intuitionist. F: Frege is a logicist. G: Gödel is a platonist. H: Hilbert is a formalist. -It is not the case that either Frege is a logicist or Brouwer is an intuitionist. Gödel being a platonist is necessary and sufficient for Brouwer being an intuitionist. Hilbert is a formalist. So, Gödel is not a platonist; however, Hilbert is a formalist.

(Short Answer)

4.8/5

(32)

Question 10

Note: the solutions to most of the multiple choice questions in these sections use what call the standard assignment of truth values to atomic propositions. The standard assignment of truth values assigns the values given here to the variables in the wffs in the exercises, when read left to right. So, the first variable in the formula read left to right gets the α assignment; the second variable in the formula read left to right (if any) gets the β assignment; the third variable in the formula read left to right (if any) gets the γ assignment; and the fourth variable in the formula read left to right (if any) gets the δ assignment. For exercises with only one propositional variable, the standard assignment is: \alpha 1 0 For exercises with two propositional variables, the standard assignment is: 1 1 1 0 0 1 0 0 For exercises with three propositional variables, the standard assignment is: \alpha \beta \gamma 1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0 For exercises with four propositional variables, the standard assignment is: \alpha \beta \gamma \delta 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 Complete truth tables for each of the following propositions. -A ? [(?B $\lor$ A) ? ?A]

(Essay)

4.8/5

(29)

Question 11

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, choose an option which presents a counterexample. (There may be other counterexamples as well.) -E ≡ F F ⊃ ∼E / E

(Multiple Choice)

4.9/5

(24)

Question 12

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, specify a counterexample. -I ⊃ J ∼(J • I) / J ⊃ I

(Essay)

4.8/5

(32)

Question 13

Note: the solutions to most of the multiple choice questions in these sections use what call the standard assignment of truth values to atomic propositions. The standard assignment of truth values assigns the values given here to the variables in the wffs in the exercises, when read left to right. So, the first variable in the formula read left to right gets the α assignment; the second variable in the formula read left to right (if any) gets the β assignment; the third variable in the formula read left to right (if any) gets the γ assignment; and the fourth variable in the formula read left to right (if any) gets the δ assignment. For exercises with only one propositional variable, the standard assignment is: \alpha 1 0 For exercises with two propositional variables, the standard assignment is: \alpha 1 1 1 0 0 1 0 0 For exercises with three propositional variables, the standard assignment is: \alpha \beta \gamma 1 1 1 1 1 0 1 0 1 1 0 0e 0 1 1 0 1 0 0 0 1 0 0 0 For exercises with four propositional variables, the standard assignment is: \alpha \gamma \delta\ 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 For each of the given propositions, determine which of the given sequences properly describes the column under the main operator, given the standard assignment of truth values to atomic propositions. -(S ? ?T) ? {[V ? (?S • T)] $\lor$ [V ? (?T • S)]}

(Multiple Choice)

4.8/5

(36)

Question 14

use indirect truth tables to determine, for each given set of propositions, whether it is consistent. If the set is consistent, choose an option with a consistent valuation. (There may be other consistent valuations.) -P ≡ (Q • ∼R) P ⊃ ∼Q (∼P • Q) ⊃ S

(Multiple Choice)

4.8/5

(36)

Question 15

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, specify a counterexample. -B $\lor$ ∼C ∼∼C / ∼B

(Essay)

4.8/5

(37)

Question 16

construct a complete truth table for each of the following propositions. Then, using the truth table, classify each proposition as a tautology, a contingency, or a contradiction. Justify your answers by appeal to the meanings of those terms. -(A • ∼B) • (B $\lor$ ∼A)

(Essay)

4.8/5

(47)

Question 17

use the following key to determine which English sentence best represents the given formula of PL. A: Peirce studied logic. B: James was a pluralist. C: Dewey wrote about thirdness. D: Dewey denigrated the quest for certainty. E: Peirce emphasized education. -∼B ⊃ (∼D • ∼E)

(Multiple Choice)

4.8/5

(32)

Question 18

Assume A, B, C are true; X, Y, Z are false; and P and Q are unknown. Evaluate the truth value of each complex expression. -∼Y ⊃ [A ≡ (Y • B)]

(Short Answer)

4.8/5

(41)

Question 19

Note: the solutions to most of the multiple choice questions in these sections use what call the standard assignment of truth values to atomic propositions. The standard assignment of truth values assigns the values given here to the variables in the wffs in the exercises, when read left to right. So, the first variable in the formula read left to right gets the α assignment; the second variable in the formula read left to right (if any) gets the β assignment; the third variable in the formula read left to right (if any) gets the γ assignment; and the fourth variable in the formula read left to right (if any) gets the δ assignment. For exercises with only one propositional variable, the standard assignment is: \alpha 1 0 For exercises with two propositional variables, the standard assignment is: 1 1 1 0 0 1 0 0 For exercises with three propositional variables, the standard assignment is: \alpha \beta \gamma 1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0 For exercises with four propositional variables, the standard assignment is: \alpha \beta \gamma \delta 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 Complete truth tables for each of the following propositions. -(S ⊃ ∼T) ⊃ {[V ⊃ (∼S ⊃ T)] $\lor$ [V ⊃ (∼T ⊃ S)]}

(Essay)

4.9/5

(34)

Question 20

use indirect truth tables to determine whether each of the following arguments is valid. If the argument is invalid, specify a counterexample. -D ⊃ (E $\lor$ F) D ⊃ (G $\lor$ F) ∼(F $\lor$ H) / D ⊃ (E • G)

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, choose an option which presents a counterexample. (There may be other counterexamples as well.) -E ≡ F F ⊃ ∼E / E

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, specify a counterexample. -I ⊃ J ∼(J • I) / J ⊃ I

use indirect truth tables to determine, for each given set of propositions, whether it is consistent. If the set is consistent, choose an option with a consistent valuation. (There may be other consistent valuations.) -P ≡ (Q • ∼R) P ⊃ ∼Q (∼P • Q) ⊃ S

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, specify a counterexample. -B $\lor$ ∼C ∼∼C / ∼B

construct a complete truth table for each of the following propositions. Then, using the truth table, classify each proposition as a tautology, a contingency, or a contradiction. Justify your answers by appeal to the meanings of those terms. -(A • ∼B) • (B $\lor$ ∼A)

use the following key to determine which English sentence best represents the given formula of PL. A: Peirce studied logic. B: James was a pluralist. C: Dewey wrote about thirdness. D: Dewey denigrated the quest for certainty. E: Peirce emphasized education. -∼B ⊃ (∼D • ∼E)

Assume A, B, C are true; X, Y, Z are false; and P and Q are unknown. Evaluate the truth value of each complex expression. -∼Y ⊃ [A ≡ (Y • B)]

Introducing Logic

Inference in Propositional Logic

Monadic Predicate Logic

Full First-Order Logic

Filters

Exam 2: Propositional Logic: Syntax and Semantic

use indirect truth tables to determine whether each of the following arguments is valid. If the argument is invalid, specify a counterexample. -D ⊃ (E ∨ \lor ∨ F) D ⊃ (G ∨ \lor ∨ F) ∼(F ∨ \lor ∨ H) / D ⊃ (E • G)

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, choose an option which presents a counterexample. (There may be other counterexamples as well.) -E ≡ F F ⊃ ∼E / E

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, specify a counterexample. -I ⊃ J ∼(J • I) / J ⊃ I

use indirect truth tables to determine, for each given set of propositions, whether it is consistent. If the set is consistent, choose an option with a consistent valuation. (There may be other consistent valuations.) -P ≡ (Q • ∼R) P ⊃ ∼Q (∼P • Q) ⊃ S

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, specify a counterexample. -B ∨ \lor ∨ ∼C ∼∼C / ∼B

construct a complete truth table for each of the following propositions. Then, using the truth table, classify each proposition as a tautology, a contingency, or a contradiction. Justify your answers by appeal to the meanings of those terms. -(A • ∼B) • (B ∨ \lor ∨ ∼A)

use the following key to determine which English sentence best represents the given formula of PL. A: Peirce studied logic. B: James was a pluralist. C: Dewey wrote about thirdness. D: Dewey denigrated the quest for certainty. E: Peirce emphasized education. -∼B ⊃ (∼D • ∼E)

Assume A, B, C are true; X, Y, Z are false; and P and Q are unknown. Evaluate the truth value of each complex expression. -∼Y ⊃ [A ≡ (Y • B)]

Introducing Logic

Inference in Propositional Logic

Monadic Predicate Logic

Full First-Order Logic

Filters

use indirect truth tables to determine whether each of the following arguments is valid. If the argument is invalid, specify a counterexample. -D ⊃ (E $\lor$ F) D ⊃ (G $\lor$ F) ∼(F $\lor$ H) / D ⊃ (E • G)

Construct a complete truth table for each of the following arguments. Then, using the truth table, determine whether the argument is valid or invalid. If the argument is invalid, specify a counterexample. -B $\lor$ ∼C ∼∼C / ∼B

construct a complete truth table for each of the following propositions. Then, using the truth table, classify each proposition as a tautology, a contingency, or a contradiction. Justify your answers by appeal to the meanings of those terms. -(A • ∼B) • (B $\lor$ ∼A)