Exam 18: Game Theory and Strategic Choices
Exam 1: The Core Principles of Economics156 Questions
Exam 2: Demand: Thinking Like a Buyer165 Questions
Exam 3: Supply: Thinking Like a Seller168 Questions
Exam 4: Equilibrium: Where Supply Meets Demand191 Questions
Exam 5: Elasticity: Measuring Responsiveness182 Questions
Exam 6: When Governments Intervene in Markets265 Questions
Exam 7: Welfare and Efficiency208 Questions
Exam 8: Gains From Trade161 Questions
Exam 9: International Trade215 Questions
Exam 10: Externalities and Public Goods241 Questions
Exam 11: Labor Demand and Supply223 Questions
Exam 12: Wages, Workers, and Management154 Questions
Exam 13: Inequality, Social Insurance, and Redistribution190 Questions
Exam 14: Market Structure and Market Power216 Questions
Exam 15: Entry, Exit, and Long-Run Profitability217 Questions
Exam 16: Business Strategy148 Questions
Exam 17: Sophisticated Pricing Strategies170 Questions
Exam 18: Game Theory and Strategic Choices227 Questions
Exam 19: Decisions Involving Uncertainty201 Questions
Exam 20: Decisions With Private Information156 Questions
Exam 21: Sizing up the Economy Using Gdp204 Questions
Exam 22: Economic Growth137 Questions
Exam 23: Unemployment167 Questions
Exam 24: Inflation and Money158 Questions
Exam 25: Consumption and Saving158 Questions
Exam 26: Investment150 Questions
Exam 27: The Financial Sector137 Questions
Exam 28: International Finance and the Exchange Rate129 Questions
Exam 29: Business Cycles149 Questions
Exam 30: IS-MP Analysis: Interest Rates and Output123 Questions
Exam 31: Phillips Curve131 Questions
Exam 32: The Fed Model: Linking Interest Rates, Output, and Inflation125 Questions
Exam 33: Aggregate Demand and Aggregate Supply169 Questions
Exam 34: Monetary Policy130 Questions
Exam 35: Government Spending, Taxes, and Fiscal Policy178 Questions
Exam 36: Appendix: Aggregate Expenditure and the Multiplier78 Questions
Select questions type
Which of the following is an example of an anti-coordination game?
(Multiple Choice)
4.8/5  (42)
(42)
(Figure: Prisoners' Dilemma for Thelma and Louise) Use Figure: Prisoners' Dilemma for Thelma and Louise. Thelma and Louise are arrested and jailed for bank robbery. Given the payoff matrix in the figure, the Nash equilibrium behavior is for Thelma _____ and Louise _____.
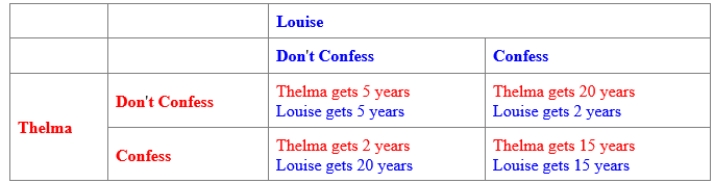
(Multiple Choice)
4.8/5  (36)
(36)
Use the table with data for Gizelle and Devin to answer the question.
Devin tries to put himself in Gizelle's place. He concludes that if he (Devin) charges $8, then Gizelle will charge _____ to earn a profit of _____.
Devin's price =\ 6 Devin's price =\ 8 Gizelle's price = Gizelle's profit =\ 3,000 Gizelle's profit =\ 6,000 \ 7 Devin's profit =\ 2,500 Devin's profit =\ 1,000 Gizelle's price = Gizelle's profit =\ 1,000 Gizelle's profit =\ 5,000 \ 9 Devin's profit =\ 5,000 Devin's profit =\ 4,000
(Multiple Choice)
4.9/5  (35)
(35)
Use the table, with data for Bella and Martin, to answer the question.
If Bella and Martin successfully cooperate, then Bella's profit will be _____, and Martin's profit will be _____.
Table: Bella's and Martin's Auto Oil Change Companies Martin's price =\ 35 Martin's price =\ 50 Bella's price = Bella's profit =\ 4,000 Bella's profit =\ 6,000 \ 40 Martin's profit =\ 3,500 Martin's profit =\ 1,000 Bella's price = Bella's profit =\ 1,000 Bella's profit =\ 5,000 \5 5 Martin's profit =\ 5,500 Martin's profit =\ 5,000
(Multiple Choice)
4.7/5  (38)
(38)
Which of the following is NOT an example of a coordination game?
(Multiple Choice)
4.9/5  (47)
(47)
While _____ markets do not necessarily lead to efficient outcomes, _____ markets tend to yield efficient outcomes.
(Multiple Choice)
4.8/5  (43)
(43)
Use the table, with data for workers and businesses, to answer the question. The payoff cells are labeled A, B, C, and D. { \text { Table: High Wage or Low Wage? } } \\
\begin{array} { | l | l | l | }
\hline & { \begin{array} { c }
\text { Businesses create unskilled } \\
\text { jobs. }
\end{array} } & { \begin{array} { c }
\text { Businesses create skilled } \\
\text { jobs. }
\end{array} } \\
\hline \text { Workers don't get training. } & \text { A. A low-skilled labor market } & \begin{array} { l }
\text { B. A shortage of skilled } \\
\text { workers }
\end{array} \\
\hline \text { Workers get training. } & \text { C. A shortage of skilled jobs } & \begin{array} { l }
\text { D. A high-skilled labor } \\
\text { market }
\end{array} \\
\hline
\end{array} The equilibria are cells _____. A high-income country would settle in _____, and a low-income country would settles in _____.
(Multiple Choice)
4.8/5  (40)
(40)
Use the table, with data for Peter and Olga, to answer the question.
Peter and Olga live near a lake with open fishing, and both have fishing boats there. They are the only two sellers in their local fish market. What is likely to be the result in a Nash equilibrium?
Table: Peter and Olga Fish in the Lake Olga fishes every day. Olga fishes two times each week. Peter fishes every day. Both Olga and Peter have smaller and smaller catches over time. Peter catches and sells more fish than Olga Peter fishes two times each week. Olga catches and sells more fish than Peter. Both Olga and Peter have large catches each fishing trip.
(Multiple Choice)
4.8/5  (35)
(35)
(Figure: Oligopoly Pricing Strategy in Wireless TV Market II) Use Figure: Oligopoly Pricing Strategy in Wireless TV Market II. If the two firms in the cable TV market collude:
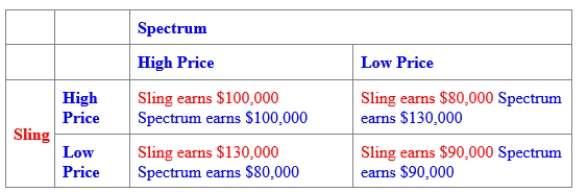
(Multiple Choice)
4.7/5  (36)
(36)
How does the Prisoner's Dilemma show that markets can deliver bad outcomes?
(Essay)
4.7/5  (44)
(44)
When using coordination games to look at the issue of bank runs, the best outcome occurs when:
(Multiple Choice)
5.0/5  (30)
(30)
The table lists the profits of two different spa chains, Elite and Supreme. The profits depend on the number of locations each chain has in a certain city.
Each chain has one location, and both owners are considering expansion. If you were the owner of Elite Day Spas, what would you do if you want to gain a first-mover advantage?
Table: Profits of Elite Day Spa and Supreme Day Spa (in thousands of dollars) Elite has one location. Elite has two locations. Elite has three locations. Supreme has one location. Supreme profits =\ 30 Elite profits =\ 30 Supreme profits =\ 15 Elite profits =\ 50 Supreme profits =\ 7 Elite profits =\ 35 Supreme has two locations. Supreme profits =\ 50 Elite profits =\ 15 Supreme profits =\ 20 Elite profits =\ 20 Supreme profits =\ 6 Elite profits =\ 10 Supreme has three locations. Supreme profits =\ 35 Elite profits =\ 7 Supreme profits =\ 10 Elite profits =\ 6 Supreme profits =\ 0 Elite profits =\ 0
(Multiple Choice)
4.8/5  (35)
(35)
How can a coordination game with multiple equilibria help explain the difference between wages in less developed countries and wages in more highly developed countries?
(Essay)
4.8/5  (34)
(34)
(Figure: Oligopoly Pricing Strategy in Wireless TV Market II) Use Figure: Oligopoly Pricing Strategy in Wireless TV Market II. The BEST response for Next Wireless:
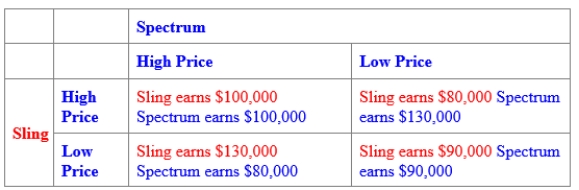
(Multiple Choice)
4.8/5  (39)
(39)
Which of the following statements regarding a Nash equilibrium is TRUE?
(Multiple Choice)
4.7/5  (41)
(41)
When a market uses a resource owned in common, then in the Nash equilibrium in that market,:
(Multiple Choice)
4.9/5  (34)
(34)
Which of the following is NOT an example of an anti-coordination game?
(Multiple Choice)
4.8/5  (43)
(43)
Use the table, with data for workers and businesses, to answer the question. The payoff cells are labeled A, B, C, and D. { \text { Table: High Wage or Low Wage? } } \\
\begin{array} { | l | l | l | }
\hline & { \begin{array} { c }
\text { Businesses create unskilled } \\
\text { jobs. }
\end{array} } & { \begin{array} { c }
\text { Businesses create skilled } \\
\text { jobs. }
\end{array} } \\
\hline \text { Workers don't get training. } & \text { A. A low-skilled labor market } & \begin{array} { l }
\text { B. A shortage of skilled } \\
\text { workers }
\end{array} \\
\hline \text { Workers get training. } & \text { C. A shortage of skilled jobs } & \begin{array} { l }
\text { D. A high-skilled labor } \\
\text { market }
\end{array} \\
\hline
\end{array} If payoffs in cells A or D are equally likely, which of the following approaches would help solve the problem and lead to D?
(Multiple Choice)
4.9/5  (34)
(34)
(Figure: Payoff Matrix for George and Garner) Use Figure: Payoff Matrix for George and Garner. The figure describes two people who sell handmade porcelain figurines in San Francisco. Both George and Garner have two strategies available to them: to produce 5,000 figurines each month or to produce 7,000 figurines each month. For both George and Garner, the BEST response is to:
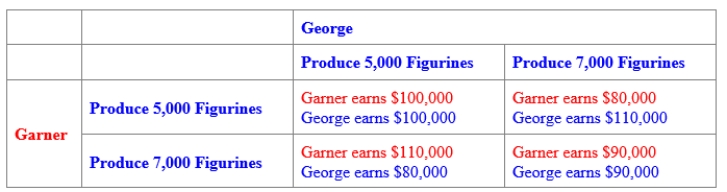
(Multiple Choice)
4.9/5  (40)
(40)
Showing 81 - 100 of 227
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)