Exam 6: Systems of Linear Equations and Inequalities
Exam 1: Equations and Inequalities169 Questions
Exam 2: Graphs102 Questions
Exam 3: Functions and Their Graphs162 Questions
Exam 4: Polynomial and Rational Functions115 Questions
Exam 5: Exponential and Logarithmic Functions133 Questions
Exam 6: Systems of Linear Equations and Inequalities87 Questions
Exam 7: Matrices109 Questions
Exam 8: Conics and Systems of Nonlinear Equations and Inequalities174 Questions
Exam 9: Sequences, Series, and Probability155 Questions
Select questions type
Select the form of the partial fraction decomposition for the given rational expression. Do not solve for the constants.
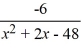
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
C
Write the form of the partial fraction decomposition for the given rational expression. Do not solve for the constants.
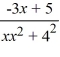
Free
(Short Answer)
4.7/5  (22)
(22)
Correct Answer:
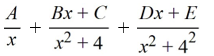
A catering company mixes cooked shredded beef with roasted Anaheim chilies to use as the filling in their house specialty burrito. How many pounds of both shredded beef that sells for$6.63 per pound and chilies that sell for $1.62 per pound must be mixed to produce 95 pounds of the mixture, witch sells for $454.50? Let b represent the number of pounds of beef and c represent the number of pounds of chilies.
(Multiple Choice)
4.9/5  (32)
(32)
Select the form of the partial fraction decomposition for the given rational expression. Do not solve for the constants.
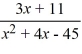
(Multiple Choice)
4.8/5  (39)
(39)
Solve the system of linear equations by graphing the following equations.
-3x + 5y = -14
2x + 5y = -24
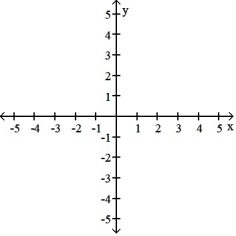
(Short Answer)
4.8/5  (38)
(38)
Solve the system of linear equations by elimination.
-4j + 3k = 3
-3j - 3k = -45
(Short Answer)
4.9/5  (29)
(29)
A candy company mixes chocolate and peanuts to create one of their signature confections. How many pounds of chocolate costing $11.82 per pound must be mixed with peanuts costing $4.37 per pound to create 50 pounds of mixture that costs $330.25? Let c represent the number of pounds of chocolate and p represent the number of pounds of peanuts.
(Short Answer)
4.7/5  (41)
(41)
Solve the system of linear equations by substitution.
2z - 7w = 18
2z - 7w = 5
(Multiple Choice)
4.8/5  (40)
(40)
Select the form of the partial fraction decomposition for the given rational expression. Do not solve for the constants.
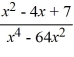
(Multiple Choice)
4.8/5  (39)
(39)
Find the solution to the system of inequalities.
5x + 2y < 5
2y < 13 - 5x
(Short Answer)
4.8/5  (38)
(38)
Solve the system of linear equations for a, b, and c.
6a - 4b + 7c = 652
A + 7b - 2c = -33
6a - 5b + 8c = 73
(Multiple Choice)
4.8/5  (31)
(31)
Solve the system of linear equations by graphing the following equations.
2x + 4y = -2
9x + 8y = 21
(Multiple Choice)
4.8/5  (36)
(36)
Solve the linear system of equations for k, m, and n.
-6k - 3m + 4n = -21
-4k + 5m - 2n = -21
-3k - 8m - 8n = -47
(Multiple Choice)
4.9/5  (36)
(36)
Showing 1 - 20 of 87
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)