Chat with AIExam 6: Systems of Linear Equations and Inequalities
Exam 1: Equations and Inequalities169 Questions
Exam 2: Graphs102 Questions
Exam 3: Functions and Their Graphs162 Questions
Exam 4: Polynomial and Rational Functions115 Questions
Exam 5: Exponential and Logarithmic Functions133 Questions
Exam 6: Systems of Linear Equations and Inequalities87 Questions
Exam 7: Matrices109 Questions
Exam 8: Conics and Systems of Nonlinear Equations and Inequalities174 Questions
Exam 9: Sequences, Series, and Probability155 Questions
Select questions type
A health food company mixes dried fruit with walnuts to make a trail mix blend. How many pounds of each ingredient must be mixed if dried fruit sells for $6.63 per pound, walnuts sell for $4.38 per pound, and the company produces 65 pounds per batch valued at $419.70? Let d represent the number of pounds of dried fruit and w the number of pounds of walnuts.
(Multiple Choice)
4.7/5 
(39)
(39) Solve the system of linear equations by substitution.
5x + 2y = -19
8x - 4y = -52
(Multiple Choice)
4.7/5 (40)
(40) Find the value of the objective function z = 2x + 6y at each of the vertices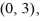 
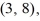
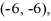and 
and then state the maximum and minimum values of the function.
and 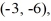and then state the maximum and minimum values of the function. (Multiple Choice)
4.8/5 (54)
(54) Select the form of the partial fraction decomposition for the given rational expression. Do not solve for the constants.
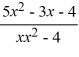
(Multiple Choice)
4.9/5 (41)
(41) Find the value of the objective function z = 8x + 4y at each of the vertices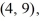 
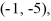
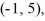and 
and then state the maximum and minimum values of the function.
and 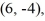and then state the maximum and minimum values of the function. (Multiple Choice)
4.9/5 (38)
(38) Solve the system of linear equations by elimination.
5d + 7f = 16
-5d - 3f = -24
(Multiple Choice)
4.9/5 (38)
(38) Employ the following supply and demand equations.
Write a system of linear inequalities corresponding to the producer surplus.
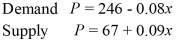Write a system of linear inequalities corresponding to the producer surplus. (Short Answer)
4.8/5 (29)
(29) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)