Exam 3: Functions and Their Graphs
Exam 1: Equations and Inequalities169 Questions
Exam 2: Graphs102 Questions
Exam 3: Functions and Their Graphs162 Questions
Exam 4: Polynomial and Rational Functions115 Questions
Exam 5: Exponential and Logarithmic Functions133 Questions
Exam 6: Systems of Linear Equations and Inequalities87 Questions
Exam 7: Matrices109 Questions
Exam 8: Conics and Systems of Nonlinear Equations and Inequalities174 Questions
Exam 9: Sequences, Series, and Probability155 Questions
Select questions type
For the given graph of a function f (x) draw the indicated function.
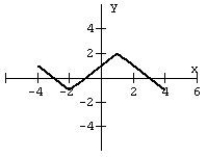 f (x + 2) - 2
f (x + 2) - 2
(Short Answer)
4.9/5  (19)
(19)
Determine if the function h(x) = 7|x| + 17 is even, odd, or neither even nor odd.
(Multiple Choice)
4.7/5  (30)
(30)
Write an equation that describes the variation. Use k as the constant of variation.
F is inversely proportional to 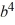 .
.
(Multiple Choice)
4.9/5  (33)
(33)
Classify the following relationship as a function or not a function.{(15, 10), (-10, -20), (-20, -16), (-14, 1), (-12, -14)}
(Multiple Choice)
4.8/5  (33)
(33)
Transform the function f (x) = -2 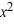 - 12x - 18 to the form f (x) = c
- 12x - 18 to the form f (x) = c 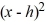 + k, where c, h, and k are constants, by completing the square.
+ k, where c, h, and k are constants, by completing the square.
(Short Answer)
4.7/5  (35)
(35)
Determine if the relationship x = 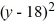 + 20 is a function. If it is a function, determine if it is a one-to-one function.
+ 20 is a function. If it is a function, determine if it is a one-to-one function.
(Multiple Choice)
4.8/5  (33)
(33)
Transform the function f (x) = 8 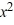 - 96x + 297 to the form f (x) = c
- 96x + 297 to the form f (x) = c 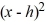 + k, where c, h, and k are constants, by completing the square.
+ k, where c, h, and k are constants, by completing the square.
(Short Answer)
4.8/5  (37)
(37)
The function f (x) = 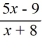 , x > -8 is a one-to-one function. Find its inverse.
, x > -8 is a one-to-one function. Find its inverse.
(Multiple Choice)
4.9/5  (31)
(31)
Find the average rate of change for the function
f (x) = 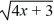 over the range x = 3 to x = 7. Round the answer to 3 decimal places if necessary.
over the range x = 3 to x = 7. Round the answer to 3 decimal places if necessary.
(Short Answer)
4.9/5  (33)
(33)
The graph of y = 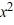 is shifted up 8 and to the left 13. Write the resulting function.
is shifted up 8 and to the left 13. Write the resulting function.
(Multiple Choice)
4.7/5  (34)
(34)
Determine if the function h(x) = 7|x + 10| is even, odd, or neither even nor odd.
(Multiple Choice)
4.9/5  (33)
(33)
Given the function G(t) = 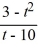 , state the domain in interval notation.
, state the domain in interval notation.
(Multiple Choice)
4.9/5  (33)
(33)
Write an equation that describes the variation.
s varies inversely with both x and the square root of q. s = 47 when x = 18 and q = 1.
(Short Answer)
4.9/5  (37)
(37)
Given the function h(t) = 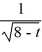 , state the domain in interval notation.
, state the domain in interval notation.
(Multiple Choice)
4.9/5  (28)
(28)
Determine if the relationship f = {(18, 12), (2, 1), (-8, 1), (-20, -3)} is a one-to-one function.
(Multiple Choice)
4.9/5  (35)
(35)
Determine if the function in the graph is even, odd, or neither:
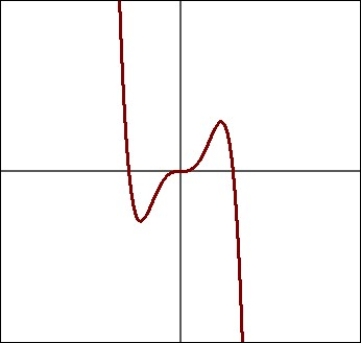
(Multiple Choice)
4.8/5  (30)
(30)
A projectile is fired straight up from an initial height of 230 feet, and its height is a function of time, h(t) = -16 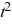 + 128t + 230 where h is the height in feet and t is the time in second with t = 0 corresponding to the instant it launches. What is the height 4 seconds after launch?
+ 128t + 230 where h is the height in feet and t is the time in second with t = 0 corresponding to the instant it launches. What is the height 4 seconds after launch?
(Short Answer)
4.9/5  (28)
(28)
Write an equation that describes the variation. Use k as the constant of variation.
f varies inversely with both 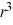 and
and  .
.
(Short Answer)
4.8/5  (30)
(30)
Given the functions f (x) = 3x + 6 and g(x) = -6x + 8, find (f + g)(x).
(Multiple Choice)
4.8/5  (40)
(40)
In physics, the inverse square law states that any physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity. In particular, the intensity of light radiating from a point source is inversely proportional to the square of the distance from the source. Below is a table of average distances from the Sun:
 The solar radiation on the Earth is approximately 1560 watts per square meter. How much solar radiation is there on Mercury? Round to the nearest hundred watts per square meter.
The solar radiation on the Earth is approximately 1560 watts per square meter. How much solar radiation is there on Mercury? Round to the nearest hundred watts per square meter.
(Multiple Choice)
4.9/5  (43)
(43)
Showing 101 - 120 of 162
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)