Exam 4: The Laws of Exponents and Logarithms: Measuring the Universe
Exam 1: An Introduction to Data and Functions149 Questions
Exam 2: Rates of Change and Linear Functions215 Questions
Exam 3: When Lines Meet: Linear Systems81 Questions
Exam 4: The Laws of Exponents and Logarithms: Measuring the Universe201 Questions
Exam 5: Growth and Decay: An Introduction to Exponential Functions146 Questions
Exam 6: Logarithmic Links: Logarithmic and Exponential Functions108 Questions
Exam 7: Power Functions109 Questions
Exam 8: Quadratics and the Mathematics of Motion127 Questions
Exam 9: New Functions From Old137 Questions
Select questions type
Simplify the expression. Express your answer using only positive exponents and evaluate whenever possible.
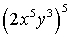
(Short Answer)
4.8/5  (41)
(41)
Use scientific notation to perform each computation. Write your answers in scientific notation.
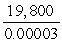
(Short Answer)
4.8/5  (41)
(41)
Rewrite the expression using fractional exponents. Do not simplify.
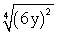
(Short Answer)
4.9/5  (35)
(35)
Simplify the expression. Express your answer using only positive exponents.
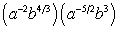
(Short Answer)
4.9/5  (40)
(40)
Simplify the expression. Express your answer using only positive exponents.
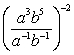
(Short Answer)
4.7/5  (34)
(34)
Use scientific notation to perform each computation. Write your answers in scientific notation.
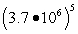
(Short Answer)
4.9/5  (29)
(29)
Use scientific notation to perform each computation. Write your answers in scientific notation.
(0.0067) (0.0016)
(Short Answer)
4.8/5  (40)
(40)
Simplify the expression. Express your answer using only positive exponents.
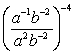
(Short Answer)
4.8/5  (36)
(36)
Assume all variables represent positive quantities and simplify.
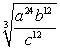
(Short Answer)
4.8/5  (42)
(42)
Use scientific notation to perform each computation. Write your answers in scientific notation.
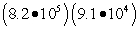
(Short Answer)
4.8/5  (30)
(30)
Solve for x:
log (2x) = 6.9
Round the answer to 4 decimal places.
(Short Answer)
4.9/5  (29)
(29)
Simplify the expression. Express your answer using only positive exponents.
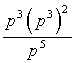
(Short Answer)
4.9/5  (36)
(36)
The time it takes for one complete swing of a pendulum is called the period of its motion. The period T (in seconds) of a swinging pendulum is found using the formula 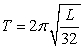 m where L is the length of the pendulum in feet and 32 is the acceleration of gravity in feet per second.
Find the period of a pendulum whose length is 1 ft 4 in. (Round the answer to 3 decimal places.)
m where L is the length of the pendulum in feet and 32 is the acceleration of gravity in feet per second.
Find the period of a pendulum whose length is 1 ft 4 in. (Round the answer to 3 decimal places.)
(Short Answer)
4.8/5  (36)
(36)
Simplify the expression. Express your answer using only positive exponents.
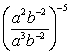
(Short Answer)
4.8/5  (32)
(32)
Showing 61 - 80 of 201
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)