Exam 8: Torque and Angular Momentum
Exam 1: Introduction39 Questions
Exam 2: Motion Along a Line27 Questions
Exam 3: Motion in a Plane24 Questions
Exam 4: Force and Newtons Laws of Motion40 Questions
Exam 5: Circular Motion43 Questions
Exam 6: Conservation of Energy35 Questions
Exam 7: Linear Momentum44 Questions
Exam 8: Torque and Angular Momentum61 Questions
Exam 9: Fluids56 Questions
Exam 10: Elasticity and Oscillations53 Questions
Exam 11: Waves41 Questions
Exam 12: Sound34 Questions
Exam 13: Temperature and the Ideal Gas56 Questions
Exam 14: Heat58 Questions
Exam 15: Thermodynamics24 Questions
Exam 16: Electric Forces and Fields38 Questions
Exam 17: Electric Potential30 Questions
Exam 18: Electric Current and Circuits36 Questions
Exam 19: Magnetic Forces and Fields33 Questions
Exam 20: Electromagnetic Induction20 Questions
Exam 21: Alternating Current10 Questions
Exam 22: Electromagnetic Waves29 Questions
Exam 23: Reflection and Refraction of Light16 Questions
Exam 24: Optical Instruments14 Questions
Exam 25: Interference and Diffraction21 Questions
Exam 26: Relativity22 Questions
Exam 27: Early Quantum Physics and the Photon18 Questions
Exam 28: Quantum Physics22 Questions
Exam 29: Nuclear Physics36 Questions
Exam 30: Particle Physics7 Questions
Select questions type
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the Z-axis, perpendicular to the X-Y plane, is
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
A
A solid cylinder with a radius has a moment of inertia of . If a torque of is applied to the object, the angular acceleration is
Free
(Multiple Choice)
5.0/5  (36)
(36)
Correct Answer:
B
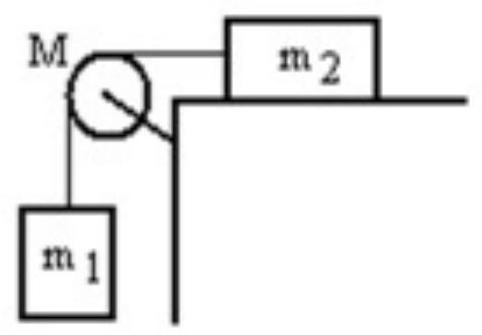
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the tension in the string attached to ?
Free
(Multiple Choice)
4.9/5  (44)
(44)
Correct Answer:
D
A wrench is used to generate a torque at a bolt. A force of is applied at the end of the wrench at an angle of 70.0 degrees. The torque generated at the bolt is
(Multiple Choice)
4.7/5  (38)
(38)
A hollow sphere of radius starts from rest and rolls without slipping down a 30.0 degree incline. The acceleration of the center of mass of the hollow sphere is
(Multiple Choice)
4.7/5  (36)
(36)
A mass is located at , a mass is located at , and a mass is located at . The center of gravity of the system of masses is
(Multiple Choice)
4.9/5  (36)
(36)
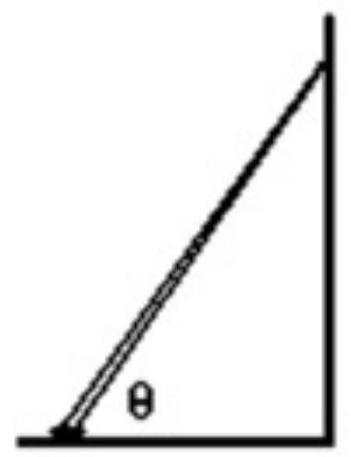
A ladder that is long is placed against a wall at an angle theta. The center of gravity of the ladder is at a point from the base of the ladder. The coefficient of static friction at the base of the ladder is 0.800 . There is no friction between the wall and the ladder. What is the minimum angle the ladder must make with the horizontal for the ladder not to slip and fall?
(Multiple Choice)
4.8/5  (42)
(42)
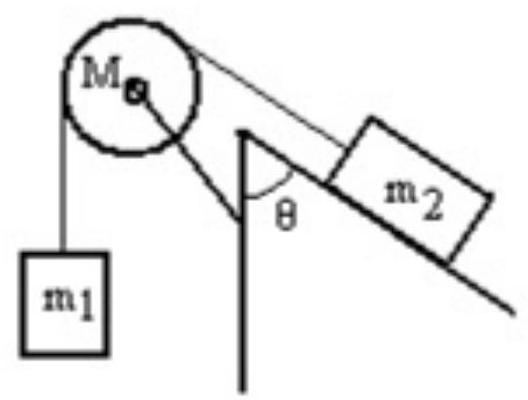
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless incline as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is is , and the angle is 60.0 degrees, then what is the acceleration of ?
(Multiple Choice)
4.7/5  (36)
(36)
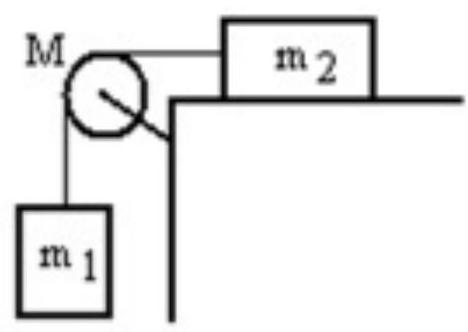
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and is , then what is the downward acceleration of ?
(Multiple Choice)
4.9/5  (26)
(26)
A wrench is used to generate a torque at a bolt. A force of is applied perpendicularly at the end of the wrench. The torque generated at the bolt is
(Multiple Choice)
4.8/5  (41)
(41)
A hollow cylinder of radius starts from rest and rolls without slipping down a 30.0 degree incline. The acceleration of the center of mass of the cylinder is
(Multiple Choice)
4.9/5  (34)
(34)
A mass is located at and a mass is located at , ). The center of gravity of the system of masses is
(Multiple Choice)
4.9/5  (39)
(39)
A ladder that is long is placed against a wall at an angle theta. The center of gravity of the ladder is at a point from the base of the ladder. The coefficient of static friction at the base of the ladder is 0.400 . There is no friction between the wall and the ladder. What is the minimum angle the ladder must make with the horizontal for the ladder not to slip and fall?
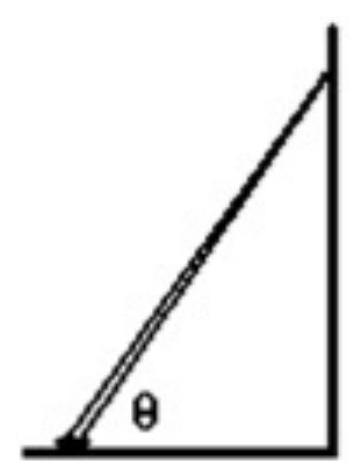
(Multiple Choice)
4.8/5  (35)
(35)
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the tension in the string that is attached to ?
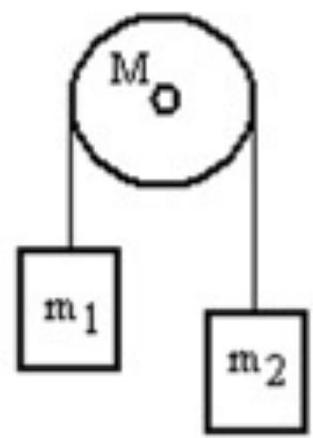
(Multiple Choice)
4.8/5  (38)
(38)
A solid sphere ( is spinning with an angular velocity of . The diameter of the sphere is . The rotational kinetic energy of the spinning sphere is
(Multiple Choice)
4.9/5  (37)
(37)
A object has a moment of inertia of . What torque is needed to give the object an angular acceleration of ?
(Multiple Choice)
5.0/5  (40)
(40)
A solid sphere with a diameter of is rotating at an angular velocity of 5.0 . The angular momentum of the rotating sphere is
(Multiple Choice)
4.9/5  (37)
(37)
A mass is located at , a mass is located at , and a mass is located at . The center of gravity of the system of masses is
(Multiple Choice)
4.8/5  (42)
(42)
The rotational inertia of a thin rod about one end is . What is the rotational inertia of the same rod about a point located from the end?
(Multiple Choice)
4.9/5  (40)
(40)
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the Y-axis, perpendicular to the Z-X plane, is
(Multiple Choice)
4.9/5  (32)
(32)
Showing 1 - 20 of 61
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)