Exam 8: Torque and Angular Momentum
Exam 1: Introduction39 Questions
Exam 2: Motion Along a Line27 Questions
Exam 3: Motion in a Plane24 Questions
Exam 4: Force and Newtons Laws of Motion40 Questions
Exam 5: Circular Motion43 Questions
Exam 6: Conservation of Energy35 Questions
Exam 7: Linear Momentum44 Questions
Exam 8: Torque and Angular Momentum61 Questions
Exam 9: Fluids56 Questions
Exam 10: Elasticity and Oscillations53 Questions
Exam 11: Waves41 Questions
Exam 12: Sound34 Questions
Exam 13: Temperature and the Ideal Gas56 Questions
Exam 14: Heat58 Questions
Exam 15: Thermodynamics24 Questions
Exam 16: Electric Forces and Fields38 Questions
Exam 17: Electric Potential30 Questions
Exam 18: Electric Current and Circuits36 Questions
Exam 19: Magnetic Forces and Fields33 Questions
Exam 20: Electromagnetic Induction20 Questions
Exam 21: Alternating Current10 Questions
Exam 22: Electromagnetic Waves29 Questions
Exam 23: Reflection and Refraction of Light16 Questions
Exam 24: Optical Instruments14 Questions
Exam 25: Interference and Diffraction21 Questions
Exam 26: Relativity22 Questions
Exam 27: Early Quantum Physics and the Photon18 Questions
Exam 28: Quantum Physics22 Questions
Exam 29: Nuclear Physics36 Questions
Exam 30: Particle Physics7 Questions
Select questions type
A grinding wheel has a mass of and moment of inertia of . A torque of is applied to the grinding wheel. If the wheel starts from rest, what is the angular momentum of the wheel after 5.0 seconds?
(Multiple Choice)
5.0/5  (32)
(32)
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the downward acceleration of ?
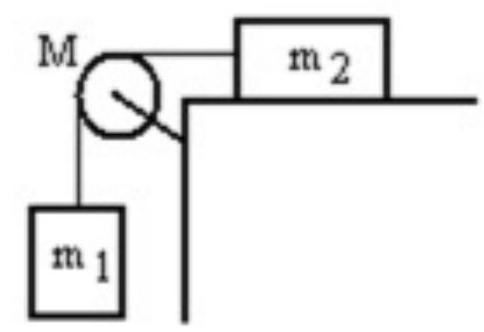
(Multiple Choice)
4.7/5  (32)
(32)
A torque of is applied to a bolt. The bolt rotates through an angle of 360 degrees. The work done in turning the bolt is
(Multiple Choice)
4.9/5  (38)
(38)
A ladder that is long is placed against a wall at an angle theta. The center of gravity of the ladder is at a point from the base of the ladder. The coefficient of static friction at the base of the ladder is 0.800 . There is no friction between the wall and the ladder. What is the vertical force of the ground on the ladder?
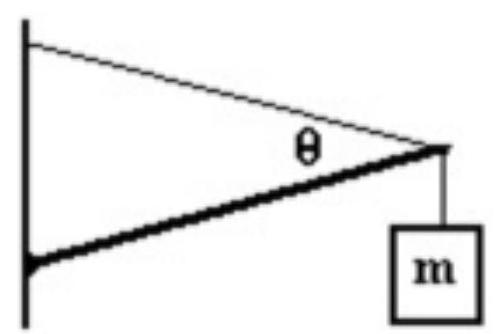
(Multiple Choice)
4.8/5  (29)
(29)
What is the rotational inertia of a solid iron disk of mass with a thickness of and radius of , about an axis perpendicular to the disk and passing through its center?
(Multiple Choice)
4.7/5  (33)
(33)
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and is , then what is the downward acceleration of ?
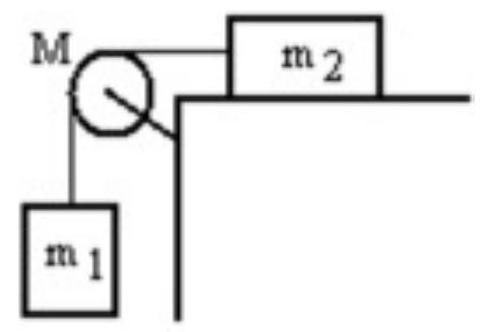
(Multiple Choice)
4.9/5  (32)
(32)
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the tension in the string attached to ?
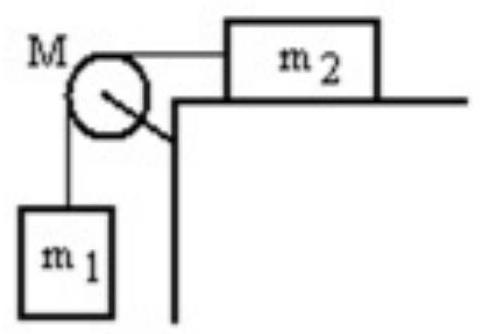
(Multiple Choice)
4.8/5  (44)
(44)
A hollow sphere is spinning with an angular velocity of . The diameter of the sphere is . The rotational kinetic energy of the spinning sphere is
(Multiple Choice)
4.8/5  (34)
(34)
A person rides a bicycle along a straight road. From the point of view of the rider, what's the direction of the angular momentum vector of the front wheel?
(Multiple Choice)
4.9/5  (40)
(40)
The rotational inertia of a thin rod about one end is . What is the rotational inertia of the same rod about a point located from the end?
(Multiple Choice)
4.8/5  (32)
(32)
An object has a moment of inertia of . If a torque of is applied to the object, the angular acceleration is
(Multiple Choice)
4.9/5  (41)
(41)
A hollow cylinder of radius starts from rest and rolls without slipping down a 30.0 degree incline. If the length of the incline is , then the velocity of the center of mass of the cylinder at the bottom of the incline is
(Multiple Choice)
4.7/5  (42)
(42)
A sphere with a radius has a moment of inertia of . If a torque of is applied to the object, the angular acceleration is
(Multiple Choice)
4.8/5  (38)
(38)
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the tension in the string attached to ?
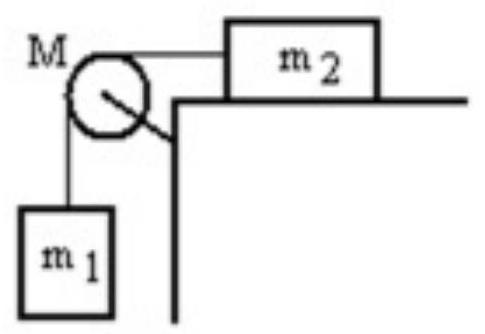
(Multiple Choice)
4.9/5  (35)
(35)
A long uniform beam of mass is supported by a wire as shown in the figure. The beam makes an angle of 10.00 degrees with the horizontal and the wire makes an angle of 30.00 degrees with the beam. A mass, , is attached to the end of the beam. What is the tension in the wire?
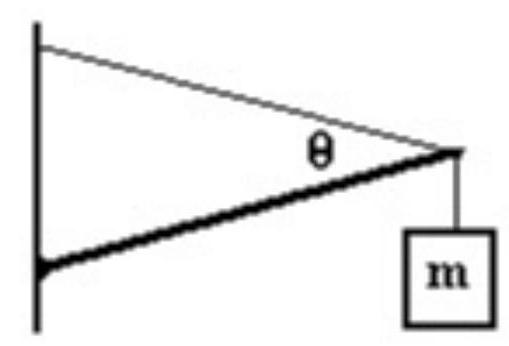
(Multiple Choice)
4.7/5  (49)
(49)
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the Z-axis, perpendicular to the plane, is
(Multiple Choice)
4.9/5  (34)
(34)
A torque of is applied to a object to give it an angular acceleration. If the angular acceleration is , then the moment of inertia is
(Multiple Choice)
4.7/5  (29)
(29)
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the tension in the string that is attached to mass ?
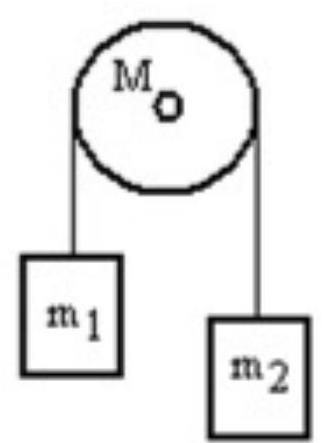
(Multiple Choice)
4.7/5  (37)
(37)
A mass is located at and a mass is located at ). The rotational inertia of this system of masses about the X-axis, perpendicular to the Z-Y plane, is
(Multiple Choice)
4.8/5  (28)
(28)
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the -axis, perpendicular to the Z-Y plane, is
(Multiple Choice)
4.8/5  (35)
(35)
Showing 21 - 40 of 61
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)