Chat with AIExam 11: Game Theory and Strategic Play
Suppose two outdoor apparel firms, L.L. Bean and Eddie Bauer, are contemplating introducing the same new product to their existing product lines. For this problem, assume that Eddie Bauer "moves" (makes this decision) first, and then L.L. Bean makes its decision. Each firm can choose to either introduce the new product or continue with the existing product. Eddie Bauer moves first, and there is "full information," meaning that each firm knows the potential payoffs (profits associated with each action). In the extensive form of this sequential game, shown in the figure below, profits (shown in parentheses in the art) are annual profits in thousands of dollars.
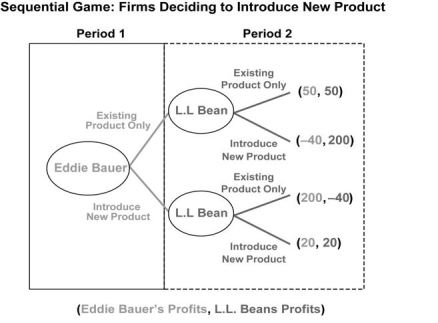Given the information above, which of the following statements is true? Explain how you arrived at your answer.
Given the information above, which of the following statements is true? Explain how you arrived at your answer.
(30) 
VerifiedB
Bill and Tom are playing a game. At each round of the game, they have to choose either Strategy X or Strategy Y. However, Tom can make a decision only after Bill has made his decision. If they both choose X, each gains $100, and if both of them choose Y, each gains $50. However, if Bill chooses X and Tom chooses Y, Bill gains $60 while Tom gains $140. Similarly, when Bill chooses Y and Tom chooses X, Tom gains $60 while Bill gains $140.
a) Draw a game tree to represent this game.
b) What type of game is being played? What is the procedure used to solve such a game?
c) What is Tom?s optimal strategy if Bill chooses Strategy X?
d) What is Bill?s payoff in equilibrium?
(33) Verifieda) The game tree for this game is shown below.
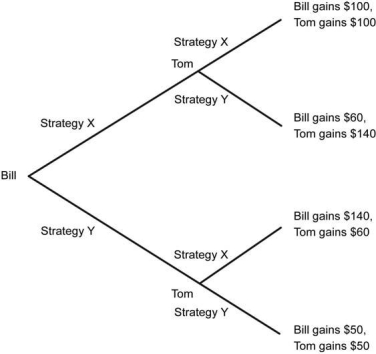b) This is an extensive-form game. The procedure that is used to solve this type of game is called backward induction. Backward induction is the procedure of solving an extensive-form game by first considering the last moverʹs decision.
c) If Bill chooses Strategy X, Tom will gain $100 by choosing Strategy X while he will gain $140 by choosing Strategy Y. Therefore, Tomʹs optimal strategy is Y if Bill chooses Strategy X.
d) Tom will choose Strategy Y if Bill chooses Strategy X because it will give him a higher payoff. Tom will choose Strategy X if Bill chooses Strategy Y because it will give him a higher payoff. Given this information, Bill will choose the strategy that will give him a higher payoff. Therefore, Bill will choose Strategy Y and his payoff will be $140 in equilibrium.
Recall the trust game reported in the Evidence-Based Economics element in section 13.5. Consider the game where the trust game is played twice in succession.
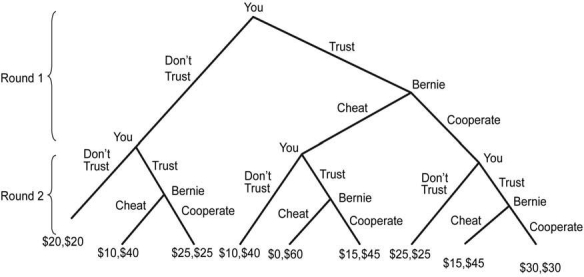Payoffs are the sum of payoff in each round. For example, suppose you choose Trust and Bernie chooses Cheat in the first round, then you choose Don?t Trust in the second round (Bernie could choose either, because it does not get to his turn anyway). Then you earn $0 and Bernie earns $30 in the first round, and you earn $10 and Bernie earns $10 in the second round, so that your total payoff is $10 and Bernie?s is $40.
a) Apply backward induction to this game. How do you and Bernie behave in the two-round version?
b) What would be the backward induction solution if the trust game is repeated three times? Four times? Twenty thousand times? Does this agree with what you read in the Evidence-Based Economics element in section 13.5?
Payoffs are the sum of payoff in each round. For example, suppose you choose Trust and Bernie chooses Cheat in the first round, then you choose Don?t Trust in the second round (Bernie could choose either, because it does not get to his turn anyway). Then you earn $0 and Bernie earns $30 in the first round, and you earn $10 and Bernie earns $10 in the second round, so that your total payoff is $10 and Bernie?s is $40.
a) Apply backward induction to this game. How do you and Bernie behave in the two-round version?
b) What would be the backward induction solution if the trust game is repeated three times? Four times? Twenty thousand times? Does this agree with what you read in the Evidence-Based Economics element in section 13.5? (36) Verifieda) In the second round, no matter what happened in the first round, Bernie has no incentive to cooperate because there is no more round. Knowing this, you would rationally choose not to trust Bernie. Knowing all this, the same thing will happen in the first round. Consequently, the backward induction outcome in each round is the same as the outcome of the one-shot play of the game: Donʹt Trust for you and Cheat for Bernie every time.
b) No matter how many times this game is repeated, you would choose not to trust Bernie, and Bernie will cheat every time in the backward induction equilibrium. This is because, at the very last round, no matter what happened in the past, Bernie has no incentive to cooperate because there is no more round, and, knowing this, you would rationally choose not to trust Bernie. Knowing all this, the same thing will happen in the second to the last round and so on. Consequently, the backward induction outcome in each round is the same as the outcome of the one-shot play of the game. However, the account in the textbook reports how real people play this type of game differently from what the theory predicts.
Another game frequently played in MBA strategy classes is the acquire a company game. The set-up of the game is as follows. Company A has only one asset, offshore oil leases. The expected profit from these leases is uniformly distributed between $0 and $100 million, so the expected value to company A is $50 million. Company B is thinking of acquiring Company A. Company B's management is more efficient than A's; specifically, the value of A's assets under B's management is 1.5 times greater. For example, the expected value of A's oil leases under B's management is 1.5 $50 million, or $75 million. Company B can submit a written bid to acquire Company A. A will review the bid, and accept or reject the offer after learning the value of the oil leases with certainty.
You are advising Company B on its potential acquisition of Company A. What is the optimal bid for Company B to submit?
(33) Contiguous states often use tax policy to attract residents, firms, and economic activity. These ʺtax competitionsʺ between states can be modeled with game theory. Suppose New Jersey currently has a state sales tax of 7 percent and Pennsylvania has a state sales tax of 6 percent. The game shown below models the effect of a reduction in each stateʹs sales tax rate to 3 percent on each stateʹs sales tax revenue. Assume the motivation of each state is to maximize tax revenue. The first number in a cell is the payoff to New Jersey; the second number is the payoff to Pennsylvania.
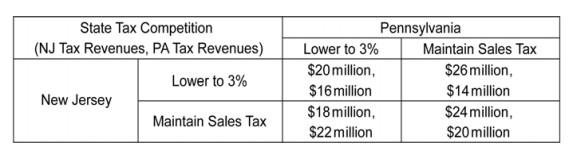-Refer to the scenario above. Is there a set of payoffs that is superior to the payoffs realized at the dominant strategy equilibrium?
-Refer to the scenario above. Is there a set of payoffs that is superior to the payoffs realized at the dominant strategy equilibrium? (34) Vladimir and Alphonso are collectors of Toy Story figurines. Each has six dollar bills to spend on three figurines-Sheriff Woody, Buzz Lightyear, and Jessie-that are put up for auction where Vlad and Alph are the only bidders. They simultaneously and independently write down their bids, in whole numbers adding up to $6, for the three figurines and give them to the auctioneer. Whoever wrote the higher number for a figurine wins it. For example, if Vlad bids ($3, $1, $2), meaning $3 for Sheriff Woody, $1 for Buzz Lightyear, and $2 for Jessie, and Alph bids ($2, $3, $1), then Vlad wins Sheriff Woody and Jessie, while Alph wins Buzz Lightyear. If there is a tie, then a fair coin is flipped to determine the winner so that each bidder has 50 percent chance of winning a figurine. Vlad and Alph consider this case as ʺwinningʺ a (1/2)figurine. Vlad and Alph care only about how many more, or less, figurines they win compared to the other.
-Refer to the scenario above. This game is an example of ________.
(43) Consider another version of the advertising game between Mountain Dew and Mello Yello. Again, each brand is deciding whether to launch an advertising campaign. These decisions will be taken simultaneously, the brands will not be cooperating, and we will assume each brand's strategist knows her own and her opponent's payoffs in all cases. The payoff matrix is listed below.
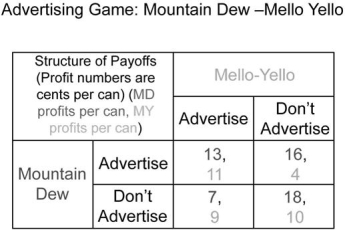Is there a Nash equilibrium in this advertising game?
Is there a Nash equilibrium in this advertising game? (38) Two rival cosmetics brands are considering launching a new product. If Firm 1 launches a product for older women while Firm 2 targets college students, Firm 1 will earn $40,000, while Firm 2 will earn $50,000. If both the firms launch a product for older women, Firm 1 will earn $20,000, while Firm 2 will earn $15,000. If Firm 1 launches a product for college students while Firm 2 targets older women, Firm 1 will earn $60,000, while Firm 2 will earn $40,000. If both firms target college students, both firms will earn $30,000. However, Firm 2 will choose its target consumers after Firm 1 has chosen its target consumers.
a) Draw a game tree to represent this situation.
b) What is the equilibrium outcome of this game?
c) Will there be a change in the equilibrium outcome if the firms make decisions simultaneously?
(30) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)