Exam 11: Random Sampling and Sampling Distributions
Exam 1: Introduction25 Questions
Exam 2: Frequency Distributions, Percentiles,34 Questions
Exam 3: Graphic Representation of Frequency Distributions25 Questions
Exam 4: Central Tendency25 Questions
Exam 5: Variability and Standard Z Scores37 Questions
Exam 6: Standard Scores and the Normal Curve27 Questions
Exam 7: Correlation38 Questions
Exam 8: Prediction40 Questions
Exam 9: Interpretive Aspects of Correlation and Regression23 Questions
Exam 10: Probability29 Questions
Exam 11: Random Sampling and Sampling Distributions24 Questions
Exam 12: Introduction to Statistical Inference: Testing Hypotheses About Single Means Z and T74 Questions
Exam 13: Interpreting the Results of Hypothesis Testing: Effect Size, Type I and Type II Errors, and Power42 Questions
Exam 14: Testing Hypotheses About the Difference Between Two Independent Groups33 Questions
Exam 15: Testing for a Difference18 Questions
Exam 16: Inference About Correlation Coefficients24 Questions
Exam 17: An Alternative to Hypothesis Testing: Confidence Intervals28 Questions
Exam 18: Testing for Differences Among Three or More Groups: One-Way Analysis of Variance and Some Alternatives49 Questions
Exam 19: Factorial Analysis of Variance30 Questions
Exam 20: Chi-Square and Inference About Frequencies27 Questions
Exam 21: Some Almost Assumption-Free Tests19 Questions
Select questions type
A sociologist engaged in research on religious attitudes tells her assistant to select a random sample of ten members for interviews from a large suburban church. The sample selected consists of nine women and one man. Upon seeing the uneven distribution of sexes in the sample, the sociologist complains, "This sample can't be random: it's almost all women." Any comments?
(Short Answer)
4.8/5  (34)
(34)
If the population consists of four scores: 5, 6, 7, and 8, and we are told that a sample of three scores from this population is: 7, 8, 8, we know that
(Multiple Choice)
4.9/5  (43)
(43)
A large population of peer ratings of physical attractiveness is approximately normal with
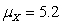 and
and 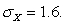 We plan to select a random sample of four ratings from this population. What is the probability of obtaining a sample mean
(a) above 6.0
(b)below 4.0
(c)between the population mean and .5 above the mean
(d)no more than .5 away from the population mean (in either direction)
(e)What sample mean has such a low value that the probability is .05 of obtaining one as low or lower?
(f)What are the centrally placed limits such that the probability is .95 that the sample mean will fall within those limits?
We plan to select a random sample of four ratings from this population. What is the probability of obtaining a sample mean
(a) above 6.0
(b)below 4.0
(c)between the population mean and .5 above the mean
(d)no more than .5 away from the population mean (in either direction)
(e)What sample mean has such a low value that the probability is .05 of obtaining one as low or lower?
(f)What are the centrally placed limits such that the probability is .95 that the sample mean will fall within those limits?
(Short Answer)
4.8/5  (35)
(35)
Showing 21 - 24 of 24
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)