Exam 5: Variability and Standard Z Scores
Exam 1: Introduction25 Questions
Exam 2: Frequency Distributions, Percentiles,34 Questions
Exam 3: Graphic Representation of Frequency Distributions25 Questions
Exam 4: Central Tendency25 Questions
Exam 5: Variability and Standard Z Scores37 Questions
Exam 6: Standard Scores and the Normal Curve27 Questions
Exam 7: Correlation38 Questions
Exam 8: Prediction40 Questions
Exam 9: Interpretive Aspects of Correlation and Regression23 Questions
Exam 10: Probability29 Questions
Exam 11: Random Sampling and Sampling Distributions24 Questions
Exam 12: Introduction to Statistical Inference: Testing Hypotheses About Single Means Z and T74 Questions
Exam 13: Interpreting the Results of Hypothesis Testing: Effect Size, Type I and Type II Errors, and Power42 Questions
Exam 14: Testing Hypotheses About the Difference Between Two Independent Groups33 Questions
Exam 15: Testing for a Difference18 Questions
Exam 16: Inference About Correlation Coefficients24 Questions
Exam 17: An Alternative to Hypothesis Testing: Confidence Intervals28 Questions
Exam 18: Testing for Differences Among Three or More Groups: One-Way Analysis of Variance and Some Alternatives49 Questions
Exam 19: Factorial Analysis of Variance30 Questions
Exam 20: Chi-Square and Inference About Frequencies27 Questions
Exam 21: Some Almost Assumption-Free Tests19 Questions
Select questions type
Each score in a sample of five raw scores is converted to a deviation score. The following are the values for four of the deviation scores: -4, +2, +3, -6. What is the value of the remaining deviation score?
(Short Answer)
4.9/5  (38)
(38)
The semi-interquartile range is most closely related to the
(Multiple Choice)
4.8/5  (43)
(43)
A set of scores has a standard deviation of 20. If 4 points were added to each score, the standard deviation would be
(Multiple Choice)
4.8/5  (37)
(37)
If a set of raw scores is positively skewed, the set of z scores derived from them will be
(Multiple Choice)
4.9/5  (30)
(30)
For the distribution of scores on a test of introversion-extroversion administered to a large group of college students, and
(high scores are in the direction of introversion). For each of the following students, convert the raw score to a z score:
(a)John, 88;
(b)George, 96;
(c)Mary, 72;
(d)Alfred, 64.
(Short Answer)
4.9/5  (33)
(33)
The scores of two groups of chimpanzees on a special problem-solving task are as follows. Group 1: 2, 7, 5, 2, 3, 8, 3. Group 2: 5, 9, 8, 5, 3. (a)Compute the standard deviations of both sets of scores, directly from deviation scores. Carry any remainders to two decimal places. (b)Compute the standard deviations of both sets of scores, using the raw score formula to obtain
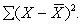
(Short Answer)
4.8/5  (35)
(35)
The major disadvantage of percentile ranks as a kind of derived score is that
(Multiple Choice)
4.8/5  (33)
(33)
The properties of the standard deviation are most closely related to those of the
(Multiple Choice)
5.0/5  (30)
(30)
For the frequency distribution of GPA's of a group of freshmen, 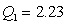 and
and
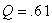 . 75% of the freshmen's GPA's fall below
. 75% of the freshmen's GPA's fall below
(Multiple Choice)
4.9/5  (36)
(36)
Use the basic definition of z scores to convert each of the following z scores back to introversion-extroversion scores from the distribution of Problem 8 (round answers to the nearest whole number):
(a)0;
(b)-2.10;
(c)1.82;
(d)-.75;
(e).25;
(f)3.10.
(Short Answer)
4.8/5  (33)
(33)
If the lowest score is 51 and the highest score is 92, the range is
(Multiple Choice)
4.8/5  (29)
(29)
Showing 21 - 37 of 37
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)