Chat with AIExam 8: Predicate Logic Semantics
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
(33) 
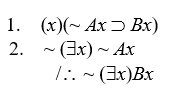
Verified Let the domain of discourse be restricted to the positive integers, and let Ax = x is an integer, Bx = x is odd. Then we get
1. All positive integers that are not integers are odd. (True, antecedent always F)
2. It is not the case that there is a positive integer that is not an integer. (True)
It is not the case that some positive integer is odd. (False)
Proving consistency
Show that the premises of the arguments below are consistent.
-
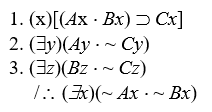
(44) VerifiedLet the domain be the positive integers, Ax = x > 1, Bx = x is odd, Cx = x is > 2:
1. All positive integers that are greater than one and odd are greater than 2.
2. Some positive integer greater than one is not greater than two.
3. Some odd positive integer is not greater than two.
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
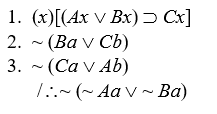
(38) VerifiedIn a two-individual universe of discourse, the argument amounts to
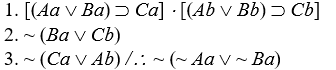Let Aa, Ba, Ca, Ab, Bb, and Cb all be false; the premises are true, the conclusion false.
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
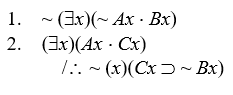
(33) Proving consistency
Show that the premises of the arguments below are consistent.
-
(42) 
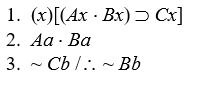
?Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
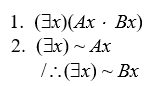
(32) General Theory
-If there are no unicorns, what is the truth value of the sentence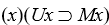 
, where Ux = x is a unicorn, and Mx = x is mortal?
, where Ux = x is a unicorn, and Mx = x is mortal? (42) Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
(43) 
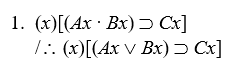
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)