Question 1

When do we mean by efficient production?

Accepted Answer

Efficient production implies that no inputs are wasted.If a given number of output is efficiently produced it is not possible to produce the same amount with less inputs.

Question 2

Suppose that additional units of capital affect the marginal productivity of labor.This is not unrealistic.Word processors increase the marginal productivity of secretaries.On the other hand,robotic equipment can completely replace a worker and,thereby,lower the marginal productivity of labor.Given this possibility,determine the conditions under which isoquants will not be convex (i.e.: concave).

Accepted Answer

The slope of the isoquant equals -MP_L/MP_K.To be concave,the slope of the isoquant becomes steeper as L increases.For this to be the case,MP_L would have to increase more than MP_K as labor increases and capital falls.That means the decrease in capital causes MP_L to rise more than the increase in labor causes MP_L to fall.The large inverse relationship implies that capital is replacing labor for this to be the case.

Question 3

A small firm in Indonesia has the following estimated production function:
ln(q)= 10 + 2.6ln(L)- 0.4(ln(L))²
Derive the firm's marginal and average product of labor as functions of q and L.What is the elasticity of output with respect to labor?

Accepted Answer

Total differentiate both sides of the function with respect to L:
(1/q)(dq/dL)= (2.6 - 0.8ln(L))(1/L)
Rearrange to get:
MP = (q/L)(2.6 - 0.8ln(L))
The AP=q/L.
The elasticity is (dq/dL)(L/q)= MP/AP = 2.6 - 0.8ln(L).

Question 4

For the following, please answer "True" or "False" and explain why.
-If inputs into production cannot be substituted for each other but have to be employed in fixed proportions,isoquants are straight,downward-sloping lines.

Accepted Answer

A) True 
 B)False

Question 5

Suppose the production function for T-shirts can be represented as q = L⁰.²⁵ K⁰.⁷⁵.Show that the isoquants for this function are convex.

Accepted Answer

The slope of the isoquant is -

Question 6

A firm has the following production function:
q = (L¹/³ + K¹/³)³
a.Determine the returns to scale for this function.
b.Determine the MRTS.
c.Determine the Elasticity of Substitution.

Accepted Answer

a.CRTS
b.M

Question 7

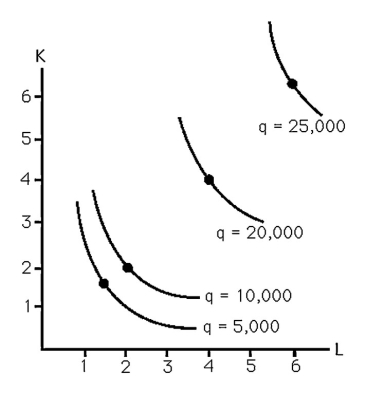-The above figure shows the isoquants for producing steel.Increasing returns to scale are

Accepted Answer

A)  present when producing less than 10,000 tons. 
B)  present when producing less than 20,000 tons. 
C)  present when producing less than 30,000 tons. 
D)  never present. 
A)  present when producing less than 10,000 tons. 
B)  present when producing less than 20,000 tons. 
C)  present when producing less than 30,000 tons. 
D)  never present.

Question 8

Long-Run Production: Two Variable Inputs
 
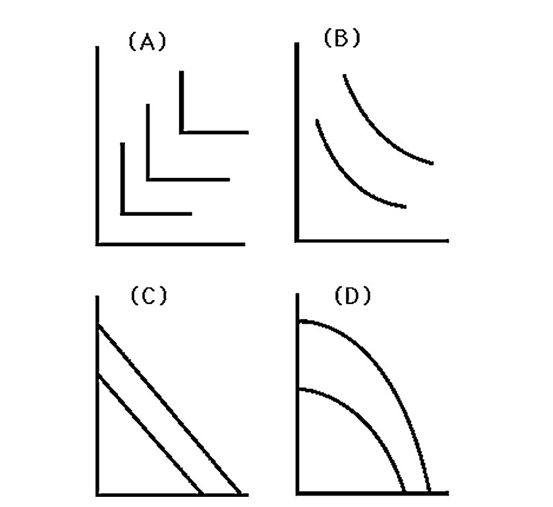-Lectures in microeconomics can be delivered either by an instructor (labor)or a movie (capital)or any combination of both.Each minute of the instructor's time delivers the same amount of information as a minute of the movie.Which graph in the above figure best represents the isoquants for lectures in microeconomics when capital per day is on the vertical axis and labor per day is on the horizontal axis?

Accepted Answer

A)  Graph A 
B)  Graph B 
C)  Graph C 
D)  Graph D 
A)  Graph A 
B)  Graph B 
C)  Graph C 
D)  Graph D

Question 9

Total product is maximized where

Accepted Answer

A)  average product is maximized. 
B)  marginal product is maximized. 
C)  average product is equal to 0. 
D)  marginal product is equal to 0. 
A)  average product is maximized. 
B)  marginal product is maximized. 
C)  average product is equal to 0. 
D)  marginal product is equal to 0.

Question 10

For the following, please answer "True" or "False" and explain why.
-If marginal productivity is decreasing as more labor is hired,then average productivity must be decreasing as well.

Accepted Answer

A) True 
 B)False

Question 11

Long-Run Production: Two Variable Inputs
 
-In the above figure,Graph D with Capital on the vertical axis and labor on the horizontal axis implies that

Accepted Answer

A)  the marginal product of labor is increasing as more labor is employed. 
B)  the marginal product of labor is decreasing as more labor is employed. 
C)  the capital and labor are perfect substitutes. 
D)  capital and labor have to be employed in fixed proportions. 
A)  the marginal product of labor is increasing as more labor is employed. 
B)  the marginal product of labor is decreasing as more labor is employed. 
C)  the capital and labor are perfect substitutes. 
D)  capital and labor have to be employed in fixed proportions.

Question 12

Provide a graph and an explanation to show that the production function Q = L⁰.⁵ K⁰.⁵ has diminishing marginal product of labor but has constant returns to scale.

Accepted Answer

@#IMG-DLM& See the above figure.The MPL = .5 ∗ L⁻⁰

Question 13

-The above figure shows the isoquants for producing steel.When producing between 10,000 and 20,000 tons there are

Accepted Answer

A)  increasing returns to scale. 
B)  decreasing returns to scale. 
C)  constant returns to scale. 
D)  economies of scale. 
A)  increasing returns to scale. 
B)  decreasing returns to scale. 
C)  constant returns to scale. 
D)  economies of scale.

Question 14

The Average Product of Labor is

Accepted Answer

A)  the change in total product resulting from an extra unit of labor, holding other factors constant. 
B)  the ratio of output to the number of workers used to produce that output. 
C)  the amount of output that can be produced by a given amount of labor. 
D)  equal to the marginal product of labor when the average product is increasing. 
A)  the change in total product resulting from an extra unit of labor, holding other factors constant. 
B)  the ratio of output to the number of workers used to produce that output. 
C)  the amount of output that can be produced by a given amount of labor. 
D)  equal to the marginal product of labor when the average product is increasing.

Question 15

The slope of the line from the origin to a given point on the curve equals

Accepted Answer

A)  the increase in output. 
B)  the change in input divided by the change in output. 
C)  the average product of the input. 
D)  the marginal product of the input. 
A)  the increase in output. 
B)  the change in input divided by the change in output. 
C)  the average product of the input. 
D)  the marginal product of the input.

Question 16

Let the production function be q = ALᵃKᵇ.Returns to scale are equal to

Accepted Answer

A)  a ∗ b. 
B)  a + b. 
C)  Lᵃ + Kᵇ. 
D)  A ∗ L. 
A)  a ∗ b. 
B)  a + b. 
C)  Lᵃ + Kᵇ. 
D)  A ∗ L.

Question 17

Average productivity will fall as long as

Accepted Answer

A)  marginal productivity is falling. 
B)  it exceeds marginal productivity. 
C)  it is less than marginal productivity. 
D)  the number of workers is increasing. 
A)  marginal productivity is falling. 
B)  it exceeds marginal productivity. 
C)  it is less than marginal productivity. 
D)  the number of workers is increasing.

Question 18

Returns to scale is a concept that operates

Accepted Answer

A)  only in the short run. 
B)  only in the long run. 
C)  in both the long run and the short run. 
D)  in either the long run or the short run but never both. 
A)  only in the short run. 
B)  only in the long run. 
C)  in both the long run and the short run. 
D)  in either the long run or the short run but never both.

Question 19

Suppose the production of paved roadways can be represented as q = L⁰.⁵ + K⁰.⁵.Which of the following statements is (are)TRUE?

Accepted Answer

A)  Labor is subject to diminishing marginal productivity in the short run. 
B)  Labor and capital are imperfect substitutes. 
C)  The isoquants for paved roadways are convex. 
D)  All of the above. 
A)  Labor is subject to diminishing marginal productivity in the short run. 
B)  Labor and capital are imperfect substitutes. 
C)  The isoquants for paved roadways are convex. 
D)  All of the above.

Question 20

Long-Run Production: Two Variable Inputs
 
-Lectures in microeconomics can be delivered either by an instructor (labor)or a movie (capital)or any combination of both.Yet the it gets harder and harder to substitute more movies for an instructor the more movies are already used.Which graph in the above figure best represents the isoquants for lectures in microeconomics when capital per day is on the vertical axis and labor per day is on the horizontal axis?

Accepted Answer

A)  Graph A 
B)  Graph B 
C)  Graph C 
D)  Graph D 
A)  Graph A 
B)  Graph B 
C)  Graph C 
D)  Graph D

When do we mean by efficient production?

A small firm in Indonesia has the following estimated production function: ln(q)= 10 + 2.6ln(L)- 0.4(ln(L))² Derive the firm's marginal and average product of labor as functions of q and L.What is the elasticity of output with respect to labor?

For the following, please answer "True" or "False" and explain why. -If inputs into production cannot be substituted for each other but have to be employed in fixed proportions,isoquants are straight,downward-sloping lines.

Suppose the production function for T-shirts can be represented as q = L⁰.²⁵ K⁰.⁷⁵.Show that the isoquants for this function are convex.

A firm has the following production function: q = (L¹/³ + K¹/³)³ a.Determine the returns to scale for this function. b.Determine the MRTS. c.Determine the Elasticity of Substitution.

-The above figure shows the isoquants for producing steel.Increasing returns to scale are

Total product is maximized where

For the following, please answer "True" or "False" and explain why. -If marginal productivity is decreasing as more labor is hired,then average productivity must be decreasing as well.

Long-Run Production: Two Variable Inputs -In the above figure,Graph D with Capital on the vertical axis and labor on the horizontal axis implies that

Provide a graph and an explanation to show that the production function Q = L⁰.⁵ K⁰.⁵ has diminishing marginal product of labor but has constant returns to scale.

-The above figure shows the isoquants for producing steel.When producing between 10,000 and 20,000 tons there are

The Average Product of Labor is

The slope of the line from the origin to a given point on the curve equals

Let the production function be q = ALᵃKᵇ.Returns to scale are equal to

Average productivity will fall as long as

Returns to scale is a concept that operates

Suppose the production of paved roadways can be represented as q = L⁰.⁵ + K⁰.⁵.Which of the following statements is (are)TRUE?

Introduction

Supply and Demand

A Consumers Constrained Choice

Demand

Consumer Welfare and Policy Analysis

Costs

Competitive Firms and Markets

Properties and Applications of the Competitive Model

General Equilibrium and Economic Welfare

Monopoly and Monopsony

Pricing and Advertising

Game Theory

Oligopoly and Monopolistic Competition

Factor Markets

Uncertainty

Property Rights, externalities, rivalry, and Exclusion

Asymmetric Information

Contracts and Moral Hazards

Filters

Exam 6: Firms and Production

When do we mean by efficient production?

A small firm in Indonesia has the following estimated production function: ln(q)= 10 + 2.6ln(L)- 0.4(ln(L))² Derive the firm's marginal and average product of labor as functions of q and L.What is the elasticity of output with respect to labor?

For the following, please answer "True" or "False" and explain why. -If inputs into production cannot be substituted for each other but have to be employed in fixed proportions,isoquants are straight,downward-sloping lines.

Suppose the production function for T-shirts can be represented as q = L⁰.²⁵ K⁰.⁷⁵.Show that the isoquants for this function are convex.

A firm has the following production function: q = (L¹/³ + K¹/³)³ a.Determine the returns to scale for this function. b.Determine the MRTS. c.Determine the Elasticity of Substitution.

-The above figure shows the isoquants for producing steel.Increasing returns to scale are

Total product is maximized where

For the following, please answer "True" or "False" and explain why. -If marginal productivity is decreasing as more labor is hired,then average productivity must be decreasing as well.

Long-Run Production: Two Variable Inputs -In the above figure,Graph D with Capital on the vertical axis and labor on the horizontal axis implies that

Provide a graph and an explanation to show that the production function Q = L⁰.⁵ K⁰.⁵ has diminishing marginal product of labor but has constant returns to scale.

-The above figure shows the isoquants for producing steel.When producing between 10,000 and 20,000 tons there are

The Average Product of Labor is

The slope of the line from the origin to a given point on the curve equals

Let the production function be q = ALᵃKᵇ.Returns to scale are equal to

Average productivity will fall as long as

Returns to scale is a concept that operates

Suppose the production of paved roadways can be represented as q = L⁰.⁵ + K⁰.⁵.Which of the following statements is (are)TRUE?

Introduction

Supply and Demand

A Consumers Constrained Choice

Demand

Consumer Welfare and Policy Analysis

Costs

Competitive Firms and Markets

Properties and Applications of the Competitive Model

General Equilibrium and Economic Welfare

Monopoly and Monopsony

Pricing and Advertising

Game Theory

Oligopoly and Monopolistic Competition

Factor Markets

Uncertainty

Property Rights, externalities, rivalry, and Exclusion

Asymmetric Information

Contracts and Moral Hazards

Filters