Exam 15: Risk and Information
Exam 1: Analyzing Economic Problems 48 Questions
Exam 2: Demand and Supply Analysis 69 Questions
Exam 3: Consumer Preferences and the Concept of Utility 61 Questions
Exam 4: Consumer Choice 57 Questions
Exam 5: The Theory of Demand 67 Questions
Exam 6: Inputs and Production Functions 70 Questions
Exam 7: Costs and Cost Minimization 61 Questions
Exam 8: Cost Curves 68 Questions
Exam 9: Perfectly Competitive Markets 57 Questions
Exam 10: Competitive Markets: Applications 66 Questions
Exam 11: Monopoly and Monopsony 65 Questions
Exam 12: Capturing Surplus 58 Questions
Exam 13: Market Structure and Competition 61 Questions
Exam 14: Game Theory and Strategic Behavior 51 Questions
Exam 15: Risk and Information 63 Questions
Exam 16: General Equilibrium Theory 56 Questions
Exam 17: Externalities and Public Goods 55 Questions
Select questions type
In a first-price sealed-bid auction when bidders have private values, the best bidding strategy is to bid
Free
(Multiple Choice)
5.0/5  (40)
(40)
Correct Answer:
C
Your current disposable income is $10,000. There is a 10% chance you will get in a serious car accident, incurring damage of $1,900. (There is a 90% chance that nothing will happen.) Your utility function is , where I is income. What is the fair price of this policy?
Free
(Multiple Choice)
4.8/5  (41)
(41)
Correct Answer:
B
A fairly-priced insurance policy is one in which
Free
(Multiple Choice)
4.7/5  (27)
(27)
Correct Answer:
A
Use the following probability distribution for a lottery to answer the following questions:
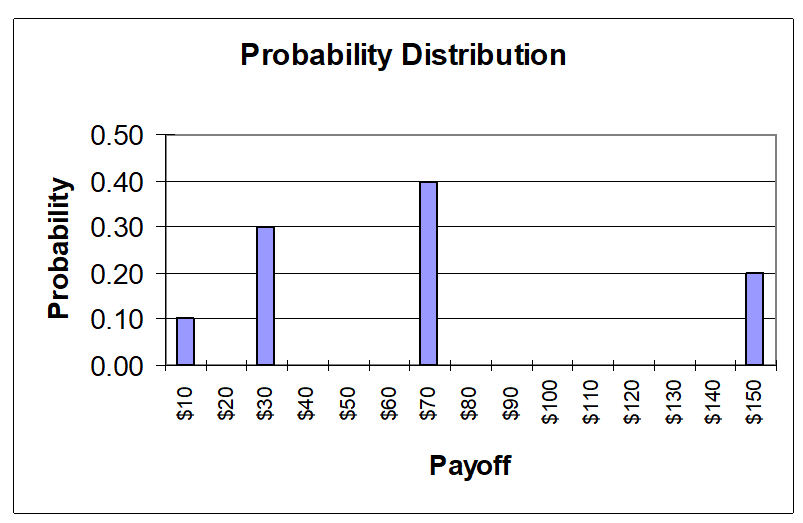 -Given the probability distribution for the lottery above, what is the expected value of this lottery?
-Given the probability distribution for the lottery above, what is the expected value of this lottery?
(Multiple Choice)
5.0/5  (42)
(42)
A good way to deal with adverse selection faced by an insurance company would not be to
(Multiple Choice)
4.8/5  (38)
(38)
Would you expect an insurance company in the "real world" to sell an insurance policy for exactly the "fairly-priced" level as defined in the text?
(Multiple Choice)
4.9/5  (37)
(37)
In general, with a first-price sealed-bid auction with private values, the Nash equilibrium bids will
(Multiple Choice)
4.8/5  (33)
(33)
A decision maker has a utility function . This decision maker is
(Multiple Choice)
4.8/5  (35)
(35)
In a second-price sealed-bid auction with private values, the winner of the auction is
(Multiple Choice)
4.9/5  (38)
(38)
Consider a lottery with four possible outcomes, A, B, C, and D. The associated payoffs are: $10, $30, $70, and $150, respectively. The probabilities are , , , and . The expected value of this lottery is
(Multiple Choice)
4.8/5  (37)
(37)
Use the following decision tree to answer the following questions:
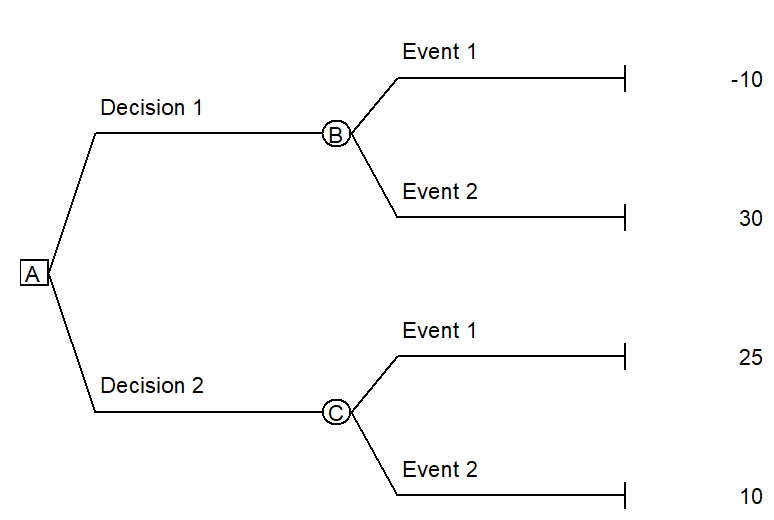 -Consider the decision tree above. If the probability of Event 1 is 30% and the probability of Event 2 is 70%, which decision alternative should the decision maker choose?
-Consider the decision tree above. If the probability of Event 1 is 30% and the probability of Event 2 is 70%, which decision alternative should the decision maker choose?
(Multiple Choice)
4.9/5  (39)
(39)
Use the following decision tree to answer the following questions:
 -If the probability of Event 1 is 30% and the probability of Event 2 is 70% in the decision tree above, the expected value of Decision 1 is
-If the probability of Event 1 is 30% and the probability of Event 2 is 70% in the decision tree above, the expected value of Decision 1 is
(Multiple Choice)
4.9/5  (41)
(41)
Consider a fairly-priced insurance policy that fully indemnifies the purchaser against their loss. This insurance policy would most likely be purchased by
(Multiple Choice)
4.8/5  (29)
(29)
Suppose a fair, two-sided coin is flipped. If it comes up heads you receive $5; if it comes up tails you lose $1. The expected value of this lottery is
(Multiple Choice)
4.7/5  (40)
(40)
Given the possible outcomes to a lottery being only the values 2, 6 with equal probabilities, calculate the expected value, variance and standard deviation?
(Multiple Choice)
4.9/5  (34)
(34)
A risk premium, RP, can be computed with the following formula, where I1 and I2 are the two payoffs to a lottery, with probabilities p and (1-p), respectively :
(Multiple Choice)
4.8/5  (38)
(38)
Suppose a fair, two-sided coin is flipped. If it comes up heads you receive $5; if it comes up tails you lose $1. The variance of this lottery is
(Multiple Choice)
4.8/5  (42)
(42)
Showing 1 - 20 of 63
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)