Exam 15: Risk and Information

An English auction is an auction wherein

Suppose you purchase a collectible baseball card from an acquaintance for $50. You think it could be worth $1,000 with a 10% probability and $0 with a 90% probability. What is your expected value for the baseball card?

Use the following probability distribution for a lottery to answer the following questions: 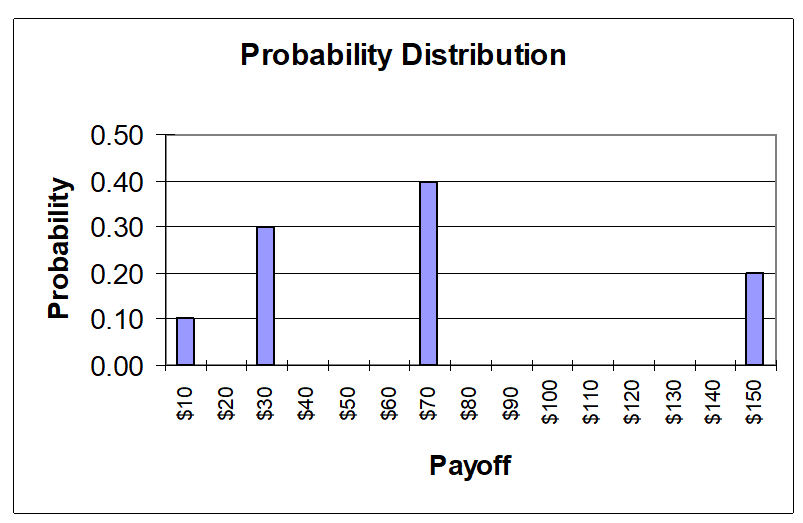-Given the probability distribution for the lottery above, what is the standard deviation of this lottery?

Large firms that can take on a number of small investment projects whose returns are independent of each other would most likely be characterized as

Which of the following statements is incorrect?

Use the following decision tree to answer the following questions: 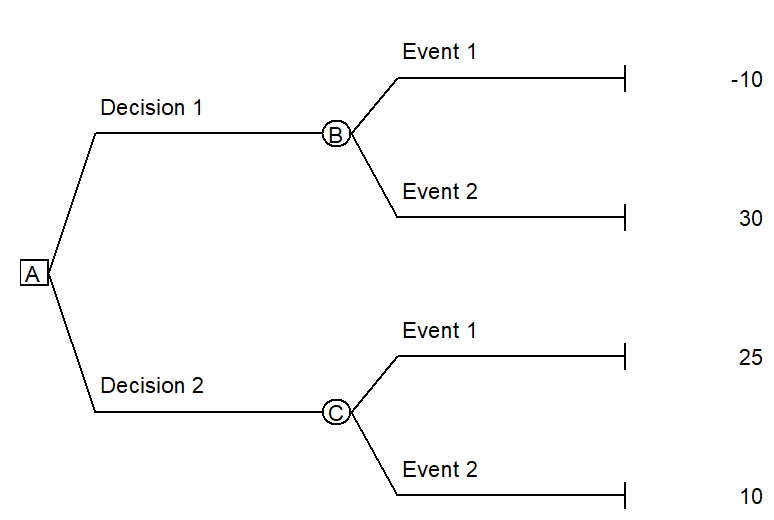-In the decision tree above, for what probability of Event 1 will Decision 1 and Decision 2 have the same expected value?

A risk premium is

An auction in which participants cry out their bids, and each participant can increase his bid until the auction ends with the highest bidder winning the object is known as

A decision-maker is faced with a choice between a lottery with a 30% chance of a payoff of $30 and a 70% chance of a payoff of $80, and a guaranteed payoff of $65. If the decision maker's utility function is U = $\sqrt { I }$ , what is the risk premium associated with this choice?

Use the decision tree along with the given probabilities to answer the following questions: Probability Event A = 30% $\quad$ Probability Event B = 70% Probability Event 1 = 58% $\quad$ Probability Event 2 = 42% Probability of Event A given that Event 1 occurs = 16% Probability of Event B given that Event 1 occurs = 84% Probability of Event A given that Event 2 occurs = 50% Probability of Event B given that Event 2 occurs = 50% -If the decision maker chooses Decision A and Event 1 occurs, which decision alternative should the decision maker choose at node D?

Consider a lottery with four equally likely outcomes, A, B, C, and D. The associated payoffs are: $10, $30, $70, and $150, respectively. The variance of this lottery is

Lotteries A and B have the same expected value, but B has larger variance. Which of the following statements is true, all else equal?

In a second-price sealed-bid auction the best bidding strategy is to bid

Consider an insurance policy with $15,000 worth of coverage. If there is a 10% chance the owner of the policy will file a claim for the $15,000 (and a 90% chance they will not file a claim), a fair price for this policy is

Your current disposable income is $10,000. There is a 10% chance you will get in a serious car accident, incurring damage of $1,900. (There is a 90% chance that nothing will happen.) Your utility function is $U = \sqrt { I }$ , where I is income. If this policy is priced at $40, what is the change in your expected utility if you purchase the policy rather than no insurance?

A decision maker can be described with utility that is only a function of income. If this function is linear, the decision maker is

A good way to deal with moral hazard faced by an insurance company would be to

Use the decision tree along with the given probabilities to answer the following questions: Probability Event A = 30% $\quad$ Probability Event B = 70% Probability Event 1 = 58% $\quad$ Probability Event 2 = 42% Probability of Event A given that Event 1 occurs = 16% Probability of Event B given that Event 1 occurs = 84% Probability of Event A given that Event 2 occurs = 50% Probability of Event B given that Event 2 occurs = 50% -If the decision maker chooses Decision B, which decision alternative should the decision maker choose at node C?

A decision maker has a utility function U = 10I. This decision maker is

Consider four lotteries, A, B, C, and D, all with an expected value of $100. The associated standard deviations of the lotteries are: A is 10, B is 15, C is 5, and D is 20. Which lottery is the riskiest?