Exam 8: Linear Programming
Exam 1: Review of Algebra470 Questions
Exam 2: Applications and More Algebra229 Questions
Exam 3: Functions and Graphs237 Questions
Exam 4: Lines parabolas and Systems218 Questions
Exam 5: Exponential and Logarithmic Functions258 Questions
Exam 6: Mathematics of Finance205 Questions
Exam 7: Matrix Algebra173 Questions
Exam 8: Linear Programming44 Questions
Exam 9: Introduction to Probability and Statistics126 Questions
Exam 10: Additional Topics in Probability45 Questions
Exam 11: Limits and Continuity241 Questions
Exam 12: Differentiation283 Questions
Exam 13: Additional Differentiation Topics191 Questions
Exam 14: Curve Sketching161 Questions
Exam 15: Integration261 Questions
Exam 16: Methods and Applications of Integration152 Questions
Exam 17: Continuous Random Variables88 Questions
Exam 18: Multivariable Calculus108 Questions
Select questions type
A company has two different locations to assemble three different models of PCs.The table below summarizes the daily production capacity,the minimum number of each type needed,and the daily operating costs for each location.Find the number of days that each location needs to operate in order to fill the orders at minimum cost. 
(Essay)
4.8/5  (27)
(27)
Use the simplex method to maximize
Z = 30x + 50y
subject to
2x + y ≤ 16
x + 2y ≤ 11
x + 3y ≤ 15
x,y ≥ 0
(Short Answer)
4.9/5  (45)
(45)
A chair company produces two models of chairs,the Sequoia and the Saratoga.The Sequoia model takes 3 hours to assemble and  hour to paint.The Saratoga model takes 2 hours to assemble and 1 hour to paint.The maximum number of hours available to assemble is 24 per day and the maximum number of hours available to paint is 8 per day.
(a)If the company earns a profit of $20 per Sequoia model and $30 per Saratoga model,find the number of models produced per day in order to maximize profit.
(b)If the company earns a profit of $30 per Sequoia model and $15 per Saratoga model,find the number of models produced per day in order to maximize profit.
(c)Suppose the company decides to upgrade the two models so it takes an additional 2 hours to detail the Sequoia and 2 hours to detail the Saratoga.The maximum number of hours available to detail is 18 per day.If the company earns a profit of $45 per Sequoia model and $35 per Saratoga model,find the number of models produced per day in order to maximize profit.
(d)Suppose the company decides to upgrade the two models so it takes an additional 2 hours to detail the Sequoia and 2 hours to detail the Saratoga.The maximum number of hours available to detail is 18 per day.If the company earns a profit of $30 per Sequoia model and $40 per Saratoga model,find the number of models produced per day in order to maximize profit.
hour to paint.The Saratoga model takes 2 hours to assemble and 1 hour to paint.The maximum number of hours available to assemble is 24 per day and the maximum number of hours available to paint is 8 per day.
(a)If the company earns a profit of $20 per Sequoia model and $30 per Saratoga model,find the number of models produced per day in order to maximize profit.
(b)If the company earns a profit of $30 per Sequoia model and $15 per Saratoga model,find the number of models produced per day in order to maximize profit.
(c)Suppose the company decides to upgrade the two models so it takes an additional 2 hours to detail the Sequoia and 2 hours to detail the Saratoga.The maximum number of hours available to detail is 18 per day.If the company earns a profit of $45 per Sequoia model and $35 per Saratoga model,find the number of models produced per day in order to maximize profit.
(d)Suppose the company decides to upgrade the two models so it takes an additional 2 hours to detail the Sequoia and 2 hours to detail the Saratoga.The maximum number of hours available to detail is 18 per day.If the company earns a profit of $30 per Sequoia model and $40 per Saratoga model,find the number of models produced per day in order to maximize profit.
(Essay)
4.8/5  (34)
(34)
To make some extra money,you make two types of picture frames,type A and type B,for sale.You have an initial start-up expense of $75.The production cost for type A is $3.60 per frame,and the production cost for type B is $5.20 per frame.The price for type A is $6.00 per frame and the price for type B is $10.00 per frame.Let x be the number of type A and y be the number of type B produced and sold.Write an inequality describing revenue less than cost.Solve the inequality and describe the region.Also,describe what this means in terms of frames.
(Essay)
4.9/5  (37)
(37)
A manufacturer produces two products,product A and product B.Both products require processing on Machines I and II.The number of hours needed to produce one unit is given by the following chart:  Machine I is available for at most 1150 hours and Machine II is available for at most 1100 hours.If the profit made on product A is $15 / unit and the profit made on product B is $30 / unit.Find the production level that will maximize profit and find the Maximum profit.
Machine I is available for at most 1150 hours and Machine II is available for at most 1100 hours.If the profit made on product A is $15 / unit and the profit made on product B is $30 / unit.Find the production level that will maximize profit and find the Maximum profit.
(Essay)
4.8/5  (41)
(41)
Use the simplex method to solve the following problem: United Blimpo Co.produces two types of exercise devices,regular and heavy-duty,each of which requires in its manufacture the use of two machines,A and B.A regular model requires the use of machine A for 2 hours and machine B for 3 hours.A heavy-duty model requires the use of machine A for 3 hours and machine B for 3 hours.Machine A can be used at most 18 hours a day and machine B can be used at most 21 hours a day.If the profits on the regular and heavy-duty models are $20 and $15,respectively,and United Blimpo Co.can sell all it produces,how many of each model should be produced per day in order to realize maximum profit? What is the maximum profit per day?
(Short Answer)
4.9/5  (31)
(31)
The dual of
Minimize
Z = 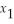 + 3
+ 3 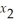 Subject to
Subject to 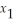 - 2
- 2 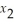 ≥ 4
3
≥ 4
3 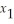 +
+ 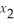 ≥ 1
≥ 1 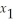 ,
, 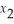 ≥ 0
Is:
≥ 0
Is:
(Multiple Choice)
4.8/5  (29)
(29)
Use the simplex method to minimize
Z = - 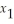 + 2
+ 2 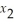 subject to
subject to 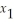 +
+ 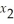 ≤ 4
5
≤ 4
5 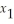 +
+ 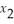 ≥ -12
2
≥ -12
2 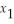 + 5
+ 5 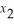 ≥ -14
3
≥ -14
3 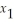 - 2
- 2 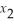 ≤ 17
≤ 17
(Essay)
4.9/5  (40)
(40)
Maximize
Z = 4x + y
subject to
-x + y ≤ 2
3x + y ≤ 18
x,y ≥ 0.
(Short Answer)
4.9/5  (39)
(39)
Use the simplex method to minimize
Z = 4 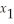 +
+ 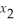 subject to
subject to 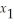 +
+ 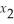 ≥ 5
≥ 5 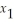 + 2
+ 2  ≥ 8
≥ 8 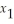 ,
, 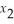 ≥ 0.
≥ 0.
(Essay)
4.9/5  (30)
(30)
Give the dual of:
Maximize
Z = 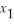 + 3
+ 3 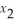 + 4
+ 4 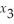 subject to
3
subject to
3 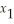 +
+ 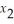 -
- 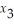 ≤ 4
4
≤ 4
4 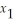 -
- 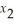 + 2
+ 2 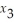 ≥ 1
≥ 1 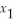 ,
, 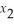 ,
, 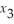 ≥ 0.
≥ 0.
(Essay)
4.7/5  (29)
(29)
Find the dual problem to the following: A company has two different locations to assemble three different models of PCs.The table below summarizes the daily production capacity,the minimum number of each type needed,and the daily operating costs for each location.What is the number of days that each location needs to operate in order to fill the orders at minimum cost. 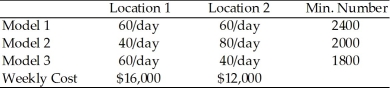
(Essay)
4.8/5  (28)
(28)
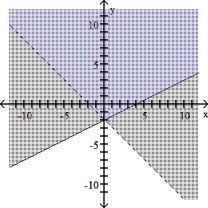
A store sells two types of calculators.In order to cover overhead,it must sell at least 40 calculators total per week,and in order to satisfy distribution requirements,it must sell at least twice as many of type II as type I.Write a system of inequalities to describe the situation.Let x be the number of type I that it sells in a week and y be the number of type II that it sells in a week.Find the region described by the system of linear inequalities.
(Essay)
4.7/5  (35)
(35)
A car rental company has $540,000 to purchase up to 25 new cars of two different models.One model costs $18,000 each and the other model costs $24,000 each.Write a system of linear inequalities to describe the situation.Let x represent the first model and y represent the second.Find the region described by the system of linear inequalities.
(Essay)
4.8/5  (33)
(33)
Showing 1 - 20 of 44
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)