Exam 6: Matrices and Determinants
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 1: Equations and Inequalities94 Questions
Exam 2: Functions and Graphs97 Questions
Exam 3: Polynomial and Rational Functions105 Questions
Exam 4: Exponential and Logarithmic Functions92 Questions
Exam 5: Systems of Equations and Inequalities94 Questions
Exam 6: Matrices and Determinants94 Questions
Exam 7: Sequences, Series, and Probability92 Questions
Select questions type
Write the system of linear equations as a matrix equation 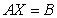 and then use Gauss-Jordan elimination on the augmented matrix
and then use Gauss-Jordan elimination on the augmented matrix 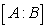 to solve for the the matrix
to solve for the the matrix 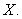
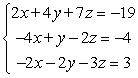
(Multiple Choice)
4.8/5  (37)
(37)
Identify the elementary row operation being performed to obtain the new row-equivalent matrix. Original Matrix New Row-Equivalent Matrix 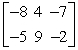
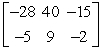
(Multiple Choice)
4.8/5  (39)
(39)
Determine whether the matrix is in row-echelon form.If it is, determine if it is also in reduced row-echelon form. 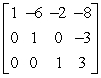
(Multiple Choice)
5.0/5  (31)
(31)
A fruit grower raises apples and peaches, which are shipped to three different outlets.The number of units of each fruit that is shipped to each outlet is shown in the matrix 
 where the first row contains the data for the number of apples shipped, the second row contains the data for the number of peaches shipped, and the columns correspond to outlets X, Y, and Z respectively.The profit per unit of apples is $4.50 and the profit per unit of peaches is $5.00.Organize the profits per unit in a matrix
where the first row contains the data for the number of apples shipped, the second row contains the data for the number of peaches shipped, and the columns correspond to outlets X, Y, and Z respectively.The profit per unit of apples is $4.50 and the profit per unit of peaches is $5.00.Organize the profits per unit in a matrix 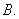
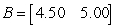 Compute
Compute 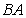 to find the profits from both crops at outlet
to find the profits from both crops at outlet 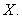
(Multiple Choice)
4.9/5  (36)
(36)
Use a determinant to determine whether the points 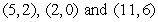 are collinear.Show all work.
are collinear.Show all work.
(Essay)
5.0/5  (29)
(29)
You invest in AAA-rated bonds, A-rated bonds, and B-rated bonds.Your average yield is 6% on AAA bonds, 9% on A bonds, and 9% on B bonds.You invest twice as much in B bonds as in A bonds.The desired system of linear equations (where 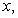
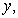 and
and 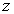 represent the amounts invested in AAA, A, and B bonds, respectively) is as follows.
represent the amounts invested in AAA, A, and B bonds, respectively) is as follows. 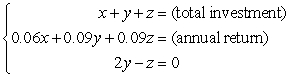 Use the inverse of the coefficient matrix of this system to find the amount invested in A bonds for the given a total investment of $45,000 and annual return of $3780.
Use the inverse of the coefficient matrix of this system to find the amount invested in A bonds for the given a total investment of $45,000 and annual return of $3780.
(Multiple Choice)
4.7/5  (31)
(31)
Write a cryptogram for the message "MERRY CHRISTMAS" using the matrix 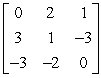 Show all your work.
Show all your work.
(Essay)
4.9/5  (31)
(31)
Solve the system of equations below by the Gaussian elimination method: 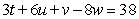
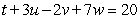
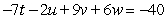
(Multiple Choice)
4.9/5  (34)
(34)
Showing 21 - 40 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)