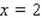Exam 5: Exponential and Logarithmic Functions
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
Sketch the graphs of the given functions on the same axes. 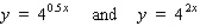
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
A
Use the definition of a logarithm to prove 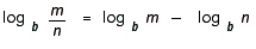 . Hint: Let
. Hint: Let 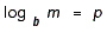 and
and 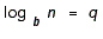 . Then,
. Then, 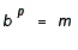 and
and 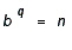 .
.
(Multiple Choice)
4.8/5  (32)
(32)
The American Court Reporting Institute finds that the average student taking Advanced Machine Shorthand, an intensive 20-week course, progresses according to the function 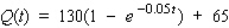 ,
, 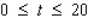 , where Q(t) measures the number of words (per minute) of dictation that the student can take in machine shorthand after t weeks in the course. Sketch the graph of the function Q and answer the following questions:
A.What is the beginning shorthand speed for the average student in this course?
B.What shorthand speed does the average student attain halfway through the course?
C.How many words per minute can the average student take after completing this course?
, where Q(t) measures the number of words (per minute) of dictation that the student can take in machine shorthand after t weeks in the course. Sketch the graph of the function Q and answer the following questions:
A.What is the beginning shorthand speed for the average student in this course?
B.What shorthand speed does the average student attain halfway through the course?
C.How many words per minute can the average student take after completing this course?
(Multiple Choice)
4.8/5  (35)
(35)
Use the facts that log 5 = 0.6990 and log 7 = 0.8451 to find the value of the logarithm. log 35
(Multiple Choice)
4.9/5  (31)
(31)
How long will it take an investment of $4,000 to double if the investment earns interest at the rate of 7% compounded continuously? Round your answer to the nearest hundredth.  __________ year(s)
__________ year(s)
(Short Answer)
4.8/5  (35)
(35)
Bernie invested a sum of money 7 year(s) ago in a savings account, which has since paid interest at the rate of 8% / year compounded quarterly. His investment is now worth $22,608.44. How much did he originally invest?
(Multiple Choice)
4.7/5  (36)
(36)
Use logarithmic differentiation to find the derivative of the function. 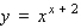
(Essay)
4.8/5  (38)
(38)
The Ehrenberg equation 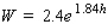 gives the relationship between the height (in meters) and the average weight W (in kilograms) for children between 5 and 13 years of age.
Round your answer to the nearest tenth.
What is the average weight of a 10-year-old child who stands at 1.62 m tall?
gives the relationship between the height (in meters) and the average weight W (in kilograms) for children between 5 and 13 years of age.
Round your answer to the nearest tenth.
What is the average weight of a 10-year-old child who stands at 1.62 m tall?  kg
Use differentials to estimate the change in the average weight of a 10-year-old child whose height increases from 1.62 m to 1.67 m.
kg
Use differentials to estimate the change in the average weight of a 10-year-old child whose height increases from 1.62 m to 1.67 m.  kg
kg
(Essay)
4.9/5  (27)
(27)
Use logarithmic differentiation to find the derivative of the function. 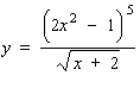
(Essay)
4.8/5  (40)
(40)
The monthly demand for a certain brand of perfume is given by the demand equation 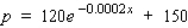 where p denotes the retail unit price (in dollars) and x denotes the quantity (in 1-oz bottles) demanded.
Find the rate of change of the price to the nearest hundredth of a cent per bottle when x = 2,000.
__________ cents per bottle
What is the price per bottle when x = 2,000.
$__________ / bottle
where p denotes the retail unit price (in dollars) and x denotes the quantity (in 1-oz bottles) demanded.
Find the rate of change of the price to the nearest hundredth of a cent per bottle when x = 2,000.
__________ cents per bottle
What is the price per bottle when x = 2,000.
$__________ / bottle
(Essay)
4.9/5  (37)
(37)
The Estradas are planning to buy a house 4 year(s) from now. Housing experts in their area have estimated that the cost of a home will increase at a rate of 8% / year during that 4-year period. If this economic prediction holds true, how much can they expect to pay for a house that currently costs $40,000? Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Given that a quantity Q(t) is described by the exponential growth function 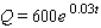 where t is measured in minutes. What is the growth constant? What quantity is present initially? Complete the table of values. Round your answers to the nearest integer.
where t is measured in minutes. What is the growth constant? What quantity is present initially? Complete the table of values. Round your answers to the nearest integer. 
(Multiple Choice)
4.7/5  (34)
(34)
Showing 1 - 20 of 278
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)