Exam 5: Exponential and Logarithmic Functions
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
Three hundred students attended the dedication ceremony of a new building on a college campus. The president of the traditionally female college announced a new expansion program, which included plans to make the college coeducational. The number of students who learned of the new program t hours later is given by the function 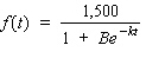 . If 600 students on campus had heard about the new program 2 hours after the ceremony, how many students had heard about the policy after 4 hours?
. If 600 students on campus had heard about the new program 2 hours after the ceremony, how many students had heard about the policy after 4 hours?
(Multiple Choice)
4.8/5  (30)
(30)
Phosphorus 32 has a half-life of 14.2 days. If 100 g of this substance are present initially, find the amount present after t days. What amount will be left after 7.1 days? How fast is the phosphorus 32 decaying when t = 7.1?
(Multiple Choice)
4.8/5  (38)
(38)
The length (in centimeters) of a typical Pacific halibut t years old is approximately 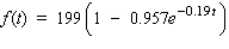 . What is the length of a typical 6-year-old Pacific halibut? How fast is the length of a typical 6-year-old Pacific halibut increasing? What is the maximum length a typical Pacific halibut can attain?
. What is the length of a typical 6-year-old Pacific halibut? How fast is the length of a typical 6-year-old Pacific halibut increasing? What is the maximum length a typical Pacific halibut can attain?
(Multiple Choice)
4.7/5  (31)
(31)
A certain piece of machinery was purchased 4 year(s) ago by Garland Mills for $400,000. Its present resale value is $256,000. Assuming that the machine's resale value decreases exponentially, what will it be 2 year(s) from now?
(Multiple Choice)
4.9/5  (32)
(32)
Find an equation of the tangent line to the graph of 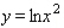 at the point
at the point 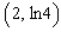 .
.
(Multiple Choice)
4.8/5  (39)
(39)
How long will it take $4,000 to grow to $7,500 if the investment earns interest at the rate of 15% / year compounded monthly? Round your answer to the nearest tenth.
__________ year(s)
(Short Answer)
5.0/5  (35)
(35)
For children between the ages of 5 and 13 years old, the Ehrenberg equation 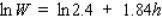 gives the relationship between the weight W (in kilograms) and the height h (in meters) of a child. Use differentials to estimate the change in the weight of a child who grows from 0.8 m to 1 m. Round the answer to the nearest tenth.
__________ kg
gives the relationship between the weight W (in kilograms) and the height h (in meters) of a child. Use differentials to estimate the change in the weight of a child who grows from 0.8 m to 1 m. Round the answer to the nearest tenth.
__________ kg
(Short Answer)
4.7/5  (34)
(34)
Find the effective rate corresponding to the given nominal rate. Round your answers to the nearest hundredth.
14% / year compounded semiannually 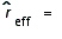 __________%
5% / year compounded quarterly
__________%
5% / year compounded quarterly 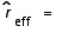 __________%
__________%
(Essay)
4.8/5  (35)
(35)
The growth rate of the bacterium, a common bacterium found in the human intestine, is proportional to its size. Under ideal laboratory conditions, when this bacterium is grown in a nutrient broth medium, the number of cells in a culture doubles approximately every 20 min. If the initial cell population is 100, determine the function Q(t) that expresses the exponential growth of the number of cells of this bacterium as a function of time t (in minutes). How long will it take for a colony of 100 cells to increase to a population of 1 million? If the initial cell population were 1,000, how would this alter the model?
(Multiple Choice)
4.8/5  (35)
(35)
Use the curve-sketching guideline, to select the graph of the function. 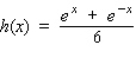
(Multiple Choice)
4.9/5  (38)
(38)
Use logarithmic differentiation to find the derivative of the function. 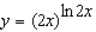
(Multiple Choice)
4.8/5  (43)
(43)
According to data obtained from the CBO, the total federal debt (in trillions of dollars) from 2001 through 2006 is given by 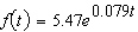
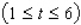 where t is measured in years, with
where t is measured in years, with 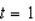 corresponding to 2001. What was the total federal debt in 2004? Round answer to three decimal places.
corresponding to 2001. What was the total federal debt in 2004? Round answer to three decimal places.
(Multiple Choice)
4.7/5  (35)
(35)
Use logarithms to solve the equation for t. Round your answer to four decimal places. 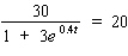 t = __________
t = __________
(Short Answer)
4.8/5  (41)
(41)
Showing 41 - 60 of 278
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)