Exam 8: Confidence Interval Estimation
Exam 1: Introduction to Data Analysis and Decision Making30 Questions
Exam 2: Describing the Distribution of a Single Variable97 Questions
Exam 3: Finding Relationships Among Variables84 Questions
Exam 4: Probability and Probability Distributions113 Questions
Exam 5: Normal, binomial, poisson, and Exponential Distributions118 Questions
Exam 6: Decision Making Under Uncertainty106 Questions
Exam 7: Sampling and Sampling Distributions92 Questions
Exam 8: Confidence Interval Estimation85 Questions
Exam 9: Hypothesis Testing85 Questions
Exam 10: Regression Analysis: Estimating Relationships97 Questions
Exam 11: Regression Analysis: Statistical Inference87 Questions
Exam 12: Time Series Analysis and Forecasting104 Questions
Exam 13: Introduction to Optimization Modeling91 Questions
Exam 14: Optimization Modeling: Applications115 Questions
Exam 15: Introduction to Simulation Modeling81 Questions
Exam 16: Simulation Models104 Questions
Select questions type
If the odds of a horse winning a race are 2 to 1,then the probability of this horse winning the race is_____.
(Multiple Choice)
4.9/5  (46)
(46)
You have been assigned to determine whether more people prefer Coke to Pepsi.Assume that roughly half the population prefers Coke and half prefers Pepsi.How large a sample would you need to take to ensure that you could estimate,with 95% confidence,the proportion of people preferring Coke within 3% of the actual value?
(Essay)
4.9/5  (36)
(36)
In general,increasing the confidence level will narrow the confidence interval,and decreasing the confidence level widens the interval.
(True/False)
4.9/5  (38)
(38)
(A)Construct a 95% confidence interval for 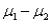 .
(B)Based on your answer to (A),are you convinced that the gaskets from shift 2 are,on average,wider than those from shift 1? Why or why not?
.
(B)Based on your answer to (A),are you convinced that the gaskets from shift 2 are,on average,wider than those from shift 1? Why or why not?
(Essay)
4.7/5  (44)
(44)
The standard error of the sampling distribution of the sample proportion 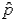 ,when the sample size n = 50 and the population proportion p = 0.25,is 0.00375.
,when the sample size n = 50 and the population proportion p = 0.25,is 0.00375.
(True/False)
4.9/5  (31)
(31)
The chi-square distribution for developing a confidence interval for a standard deviation has_____ degrees of freedom.
(Multiple Choice)
4.7/5  (33)
(33)
A 90% confidence interval estimate for a population mean 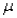 is determined to be 72.8 to 79.6.If the confidence level is reduced to 80%,the confidence interval for
is determined to be 72.8 to 79.6.If the confidence level is reduced to 80%,the confidence interval for 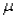 becomes narrower.
becomes narrower.
(True/False)
4.8/5  (40)
(40)
When the samples we want to compare are paired in some natural way,such as pretest/posttest for each person or husband/wife pairs,a more appropriate form of analysis is to not compare two separate variables,but their _____.
(Multiple Choice)
4.8/5  (40)
(40)
From a sample of 500 items,30 were found to be defective.The point estimate of the population proportion defective will be:
(Multiple Choice)
4.8/5  (33)
(33)
The interval estimate 18.5 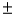 2.5 was developed for a population mean when the sample standard deviation s was 7.5.Had s equaled 15,the interval estimate would be 37
2.5 was developed for a population mean when the sample standard deviation s was 7.5.Had s equaled 15,the interval estimate would be 37 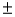 5.0.
5.0.
(True/False)
4.7/5  (33)
(33)
After calculating the sample size needed to estimate a population proportion to within 0.05,you have been told that the maximum allowable error (B)must be reduced to just 0.025.If the original calculation led to a sample size of 1000,the sample size will now have to be:
(Multiple Choice)
4.8/5  (40)
(40)
Two independent samples of sizes 50 and 50 are randomly selected from two populations to test the difference between the population means, 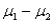 .The sampling distribution of the sample mean difference
.The sampling distribution of the sample mean difference 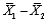 is:
is:
(Multiple Choice)
4.8/5  (33)
(33)
In developing a confidence interval for the population standard deviation 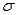 ,we make use of the fact that the sampling distribution of the sample standard deviation s is not the normal distribution or the t-distribution,but rather a right-skewed distribution called the chi-square distribution,which (for this procedure)has n - 1 degrees of freedom.
,we make use of the fact that the sampling distribution of the sample standard deviation s is not the normal distribution or the t-distribution,but rather a right-skewed distribution called the chi-square distribution,which (for this procedure)has n - 1 degrees of freedom.
(True/False)
4.8/5  (39)
(39)
The t-distribution for developing a confidence interval for a mean has _____ degrees of freedom.
(Multiple Choice)
4.9/5  (37)
(37)
(A)Compute 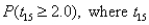 has a t-distribution with 15 degrees of freedom.
(B)Compute
has a t-distribution with 15 degrees of freedom.
(B)Compute 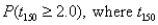 has a t-distribution with 150 degrees of freedom.
(C)How do you explain the difference between the results obtained in (A)and (B)?
(D)Compute
has a t-distribution with 150 degrees of freedom.
(C)How do you explain the difference between the results obtained in (A)and (B)?
(D)Compute 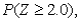 where Z is a standard normal random variable.
(E)Compare the results of (D)to the results obtained in (A)and (B).How do you explain the difference in these probabilities?
where Z is a standard normal random variable.
(E)Compare the results of (D)to the results obtained in (A)and (B).How do you explain the difference in these probabilities?
(Essay)
4.9/5  (38)
(38)
(A)Use a t - value of 2.014 to calculate a 95% confidence interval for the difference between the average female purchase and the average male purchase.Would you conclude that there is a significant difference between females and males in this case? Explain.
(B)What are the degrees of freedom for the t-multiple in this calculation? Explain how you would calculate the degrees of freedom in this case.
(C)What is the assumption in this case that allows you to use the pooled standard deviation for this confidence interval?
(Essay)
4.8/5  (31)
(31)
In past years,approximately 25% of all U.S.families purchased potato chips at least once a month.We are interested in determining the fraction of all U.S.families that currently purchase potato chips at least once a month.How many families must we survey if we want to be 99% sure that our estimate of the fraction of U.S.families currently purchasing potato chips at least once a month is accurate within 2%?
(Essay)
4.9/5  (40)
(40)
If the standard error of the sampling distribution of the sample proportion 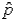 is 0.0324 for samples of size 200,then the population proportion must be 0.30.
is 0.0324 for samples of size 200,then the population proportion must be 0.30.
(True/False)
4.9/5  (32)
(32)
As the sample size increases,the t-distribution becomes more similar to the ________ distribution.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 41 - 60 of 85
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)