Exam 10: Basic Regression Analysis With Time Series Data
Exam 1: The Nature of Econometrics and Economic Data25 Questions
Exam 2: The Simple Regression Model25 Questions
Exam 3: Multiple Regression Analysis: Estimation24 Questions
Exam 4: Multiple Regression Analysis: Inference25 Questions
Exam 5: Multiple Regression Analysis: Ols Asymptotics25 Questions
Exam 6: Multiple Regression Analysis: Further Issues25 Questions
Exam 7: Multiple Regression Analysis With Qualitative Information: Binary or Dummy Variables25 Questions
Exam 8: Heteroskedasticity25 Questions
Exam 9: More on Specification and Data Problems25 Questions
Exam 10: Basic Regression Analysis With Time Series Data24 Questions
Exam 11: Further Issues in Using Ols With Time Series Data25 Questions
Exam 12: Serial Correlation and Heteroskedasticity in Time Series Regressions25 Questions
Exam 13: Pooling Cross Sections Across Time: Simple Panel Data Methods25 Questions
Exam 14: Advanced Panel Data Methods25 Questions
Exam 15: Instrumental Variables Estimation and Two Stage Least Squares25 Questions
Exam 16: Simultaneous Equations Models25 Questions
Exam 17: Limited Dependent Variable Models and Sample Selection Corrections25 Questions
Exam 18: Advanced Time Series Topics25 Questions
Exam 19: Carrying Out an Empirical Project25 Questions
Select questions type
Economic time series are outcomes of random variables.
Free
(True/False)
4.8/5  (41)
(41)
Correct Answer:
True
The model: Yt = 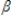 0 +
0 + 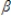 1ct + ut, t = 1,2,……., n is an example of a(n):
1ct + ut, t = 1,2,……., n is an example of a(n):
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
B
With base year 1990, the index of industrial production for the year 1999 is 112. What will be the value of the index in 1999, if the base year is changed to 1982 and the index measured 96 in 1982?
Free
(Multiple Choice)
4.7/5  (26)
(26)
Correct Answer:
B
If an explanatory variable is strictly exogenous it implies that:
(Multiple Choice)
4.9/5  (30)
(30)
Adding a time trend can make an explanatory variable more significant if:
(Multiple Choice)
4.9/5  (35)
(35)
If 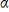 1 > 0, then yt in the linear function of time E(yt) =
1 > 0, then yt in the linear function of time E(yt) = 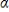 0 +
0 + 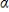 1t displays a(n):
1t displays a(n):
(Multiple Choice)
4.7/5  (29)
(29)
Which of the following is an assumption on which time series regression is based?
(Multiple Choice)
4.7/5  (38)
(38)
Which of the following rules out perfect collinearity among the regressors?
(Multiple Choice)
4.7/5  (40)
(40)
When a series has the same average growth rate from period to period, then it can be approximated by an exponential trend.
(True/False)
4.9/5  (29)
(29)
Which of the following correctly identifies a difference between cross-sectional data and time series data?
(Multiple Choice)
4.8/5  (32)
(32)
Refer to the following model. yt =  0 +
0 + 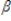 0st +
0st + 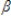 1st-1 +
1st-1 + 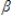 2st-2 +
2st-2 + 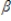 3st-3 + ut
3st-3 + ut 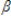 0 +
0 + 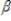 1 +
1 + 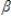 2 +
2 + 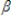 3 represents:
3 represents:
(Multiple Choice)
4.9/5  (27)
(27)
Time series regression is based on series which exhibit serial correlation.
(True/False)
4.7/5  (34)
(34)
Price indexes are necessary for turning a time series measured in real value into nominal value.
(True/False)
4.9/5  (30)
(30)
The sample size for a time series data set is the number of:
(Multiple Choice)
4.9/5  (40)
(40)
In a static model, one or more explanatory variables affect the dependent variable with a lag.
(True/False)
4.7/5  (36)
(36)
Dummy variables can be used to address the problem of seasonality in regression models.
(True/False)
4.8/5  (34)
(34)
Refer to the following model yt =  0 +
0 + 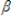 0st +
0st + 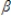 1st-1 +
1st-1 + 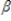 2st-2 +
2st-2 + 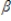 3st-3 + ut
This is an example of a(n):
3st-3 + ut
This is an example of a(n):
(Multiple Choice)
4.8/5  (29)
(29)
Showing 1 - 20 of 24
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)