True/False
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination (  )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
)of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below: 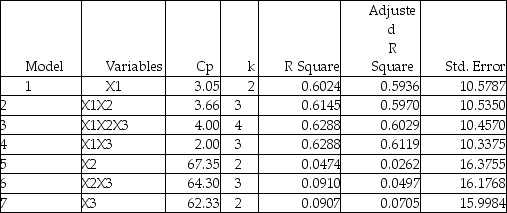 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance: 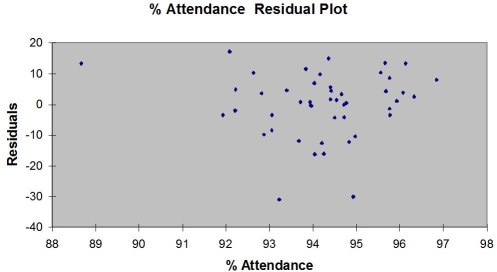 Following is the output of several multiple regression models:
Following is the output of several multiple regression models:
Model (I): 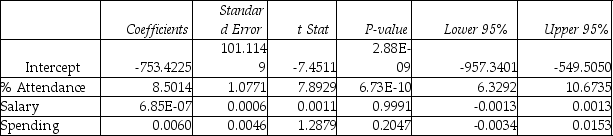 Model (II):
Model (II):  Model (III):
Model (III): 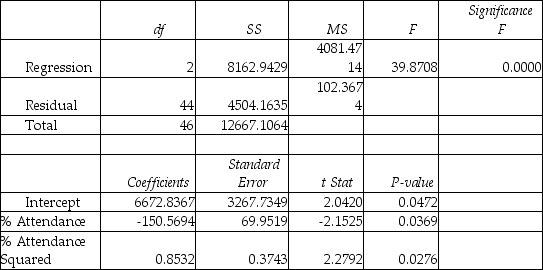
-True or False: Referring to Table 15-4,there is reason to suspect collinearity between some pairs of predictors.
Correct Answer:

Verified
Correct Answer:
Verified
Q1: True or False: So that we can
Q8: A real estate builder wishes to determine
Q25: TABLE 15-6<br>Given below are results from the
Q26: The logarithm transformation can be used<br>A)to overcome
Q29: TABLE 15-6<br>Given below are results from the
Q64: Using the best-subsets approach to model building,models
Q65: TABLE 15-1<br>A certain type of rare gem
Q71: TABLE 15-6<br>Given below are results from the
Q72: True or False: Two simple regression models
Q93: TABLE 15-1<br>A certain type of rare gem