Solved

Find All Solutions of the Following Equation in the Interval

Question 578

Multiple Choice

Find all solutions of the following equation in the interval [0, 2π) . ​ Find all solutions of the following equation in the interval [0, 2π) . ​ ​ A) B) ​ C) ​ D) ​ E) ​ ​


A) Find all solutions of the following equation in the interval [0, 2π) . ​ ​ A) B) ​ C) ​ D) ​ E) ​
B) ​ Find all solutions of the following equation in the interval [0, 2π) . ​ ​ A) B) ​ C) ​ D) ​ E) ​
C) ​ Find all solutions of the following equation in the interval [0, 2π) . ​ ​ A) B) ​ C) ​ D) ​ E) ​
D) ​ Find all solutions of the following equation in the interval [0, 2π) . ​ ​ A) B) ​ C) ​ D) ​ E) ​
E) ​ Find all solutions of the following equation in the interval [0, 2π) . ​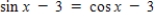 ​ A) 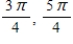B) ​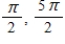 C) ​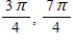 D) ​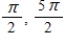 E) ​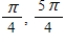

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q45: Evaluate the function f(x)= [[3x + 1]]

Q573: Place the correct symbol (<, >, or

Q574: Find the slope-intercept form of the equation

Q575: Evaluate the expression for the given value

Q576: Rewrite the expression with positive exponents and

Q577: Identify the rule(s) of algebra illustrated by

Q579: Use inverse functions where needed to find

Q580: Which of the following is a solution

Q582: Evaluate the following expression without using a

Q583: Select the graph of the function: f(x)