Solved

Use Inverse Functions Where Needed to Find All Solutions (If

Question 579

Multiple Choice

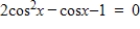
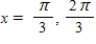
Use inverse functions where needed to find all solutions (if they exist) of the given equation on the interval [0, 2π) . ​ Use inverse functions where needed to find all solutions (if they exist) of the given equation on the interval [0, 2π) . ​ ​ A) ​ B) C) D) E) ​solution does not exist ​


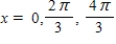
A) ​ Use inverse functions where needed to find all solutions (if they exist) of the given equation on the interval [0, 2π) . ​ ​ A) ​ B) C) D) E) ​solution does not exist
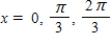
B) Use inverse functions where needed to find all solutions (if they exist) of the given equation on the interval [0, 2π) . ​ ​ A) ​ B) C) D) E) ​solution does not exist
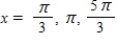
C) Use inverse functions where needed to find all solutions (if they exist) of the given equation on the interval [0, 2π) . ​ ​ A) ​ B) C) D) E) ​solution does not exist
D) Use inverse functions where needed to find all solutions (if they exist) of the given equation on the interval [0, 2π) . ​ ​ A) ​ B) C) D) E) ​solution does not exist
E) ​solution does not exist

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q5: Evaluate the function f(x)= 2[[x]] + 7

Q45: Evaluate the function f(x)= [[3x + 1]]

Q574: Find the slope-intercept form of the equation

Q575: Evaluate the expression for the given value

Q576: Rewrite the expression with positive exponents and

Q577: Identify the rule(s) of algebra illustrated by

Q578: Find all solutions of the following equation

Q580: Which of the following is a solution

Q582: Evaluate the following expression without using a

Q583: Select the graph of the function: f(x)