Solved

Consider the Quarterly Production Data (In Thousands of Units) for the XYZ

Question 128

Short Answer

Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365.
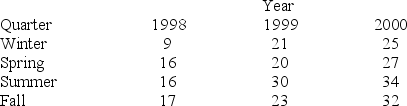Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. 1998 1999 2000 The following Minitab output gives the straight-line trend equation fitted to the deseasonalized observations. Based on the trend equation given below, calculate the trend value for each period in the time series. The regression equation is Deseasonalized = 10.1 + 1.91 × Time Based on the following deseasonalized observations (dt), a trend line was estimated.
1998
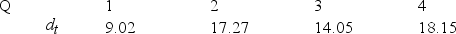Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. 1998 1999 2000 The following Minitab output gives the straight-line trend equation fitted to the deseasonalized observations. Based on the trend equation given below, calculate the trend value for each period in the time series. The regression equation is Deseasonalized = 10.1 + 1.91 × Time 1999
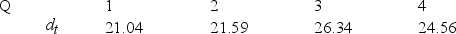Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. 1998 1999 2000 The following Minitab output gives the straight-line trend equation fitted to the deseasonalized observations. Based on the trend equation given below, calculate the trend value for each period in the time series. The regression equation is Deseasonalized = 10.1 + 1.91 × Time 2000
Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. 1998 1999 2000 The following Minitab output gives the straight-line trend equation fitted to the deseasonalized observations. Based on the trend equation given below, calculate the trend value for each period in the time series. The regression equation is Deseasonalized = 10.1 + 1.91 × Time The following Minitab output gives the straight-line trend equation fitted to the deseasonalized observations. Based on the trend equation given below, calculate the trend value for each period in the time series.
The regression equation is Deseasonalized = 10.1 + 1.91 × Time
Consider the quarterly production data (in thousands of units) for the XYZ manufacturing company below. The normalized (adjusted) seasonal factors are winter = .9982, spring = .9263, summer = 1.139, and fall = .9365. Based on the following deseasonalized observations (d<sub>t</sub>), a trend line was estimated. 1998 1999 2000 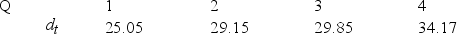The following Minitab output gives the straight-line trend equation fitted to the deseasonalized observations. Based on the trend equation given below, calculate the trend value for each period in the time series. The regression equation is Deseasonalized = 10.1 + 1.91 × Time

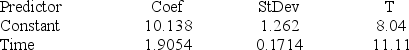
Correct Answer:

verifed

Verified

12.01, 13.91, 15.82, 17.72, 19.63, 21.54...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q123: Consider a time series with 15 quarterly

Q124: Those fluctuations that are associated with climate,

Q125: When deseasonalizing a time series observation, we

Q126: Exponential smoothing is designed to forecast time

Q127: When preparing a price index based on

Q129: Simple exponential smoothing is a forecasting method

Q130: A forecasting method that weights recent observations

Q131: When there is _ seasonal variation, the

Q132: Consider the following set of quarterly sales

Q133: The Box-Jenkins methodology can be used to