Multiple Choice
Use the change-of-base formula to rewrite the logarithm as a ratio of logarithms.Then use a graphing utility to graph the ratio.
F(x) = log4 x
A) f(x) = log x + log 4 = ln x + ln 4 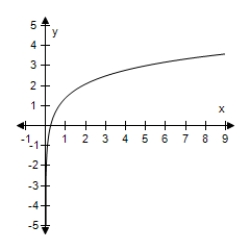
B) 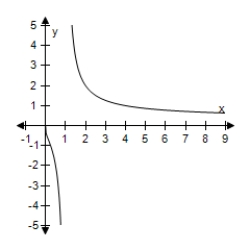
C) 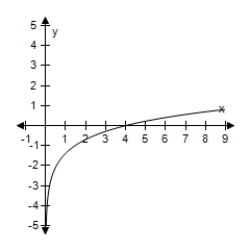
D) 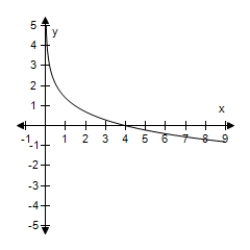
E) 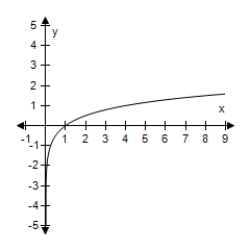
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q25: Solve the equation.Round to 3 decimal places.
Q201: Solve the exponential equation algebraically.Approximate the
Q202: Select the correct graph for the
Q203: Assume that x, y and c
Q204: $4500 is invested in an account
Q205: Condense the expression to the logarithm
Q207: Write the exponential equation in logarithmic
Q209: Select the graph of the exponential
Q210: Use a calculator to find a
Q211: Solve the exponential equation algebraically.Approximate the