Multiple Choice
Select the graph of the exponential function.
A) 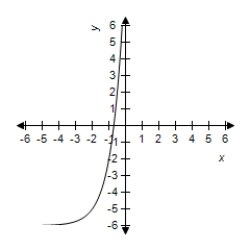
B) 
C) 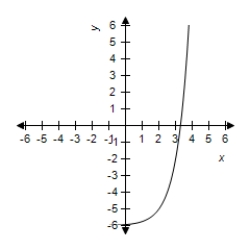
D) 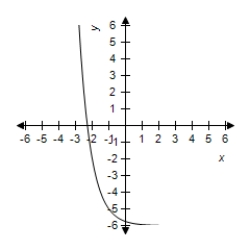
E) 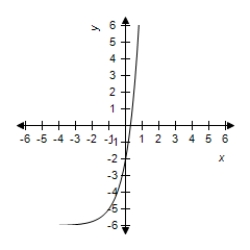
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q25: Solve the equation.Round to 3 decimal places.
Q204: $4500 is invested in an account
Q205: Condense the expression to the logarithm
Q206: Use the change-of-base formula to rewrite
Q207: Write the exponential equation in logarithmic
Q210: Use a calculator to find a
Q211: Solve the exponential equation algebraically.Approximate the
Q212: Solve the logarithmic equation algebraically.Approximate the
Q213: Evaluate the function <span class="ql-formula"
Q214: Select the graph of the function.