Multiple Choice
Use a graphing utility to determine which of the trigonometric functions is equal to the following expression.
A) y = cos x2- 2 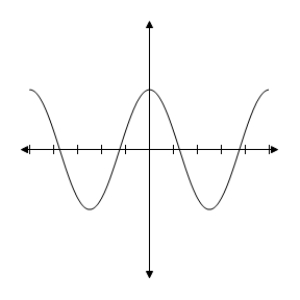 2 - 2
2 - 2
B) y = sin x2- 2 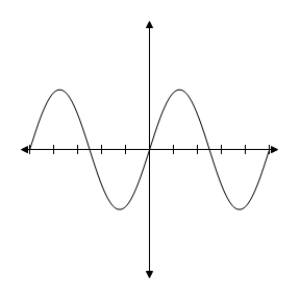 2 - 2
2 - 2
C) y = csc x4- 2 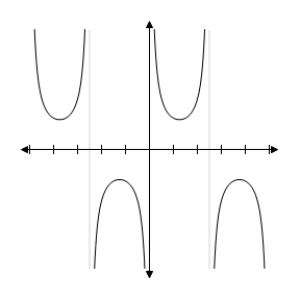 2 - 4
2 - 4
D) y = cot x4- 2 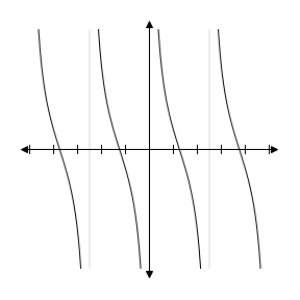 2 - 4
2 - 4
E) y = tan x4- 2 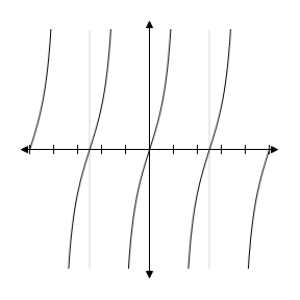 2 - 4
2 - 4
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q12: Evaluate the following expression. <br>2(1 + sin
Q16: Evaluate the following expression.(x ≠ π/2+πn,where n
Q20: A weight is attached to a
Q21: Use the half-angle formulas to simplify
Q22: Solve the multiple-angle equation. <br>
Q23: Find all solutions of the following
Q24: Use the sum-to-product formulas to find
Q26: Use the Quadratic Formula to solve
Q29: Use fundamental identities to simplify the
Q30: Use a graphing utility to graph