Multiple Choice
Write the complex number in trigonometric form. 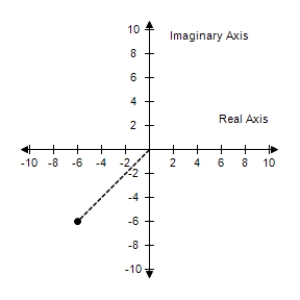
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q19: Determine whether the Law of Sines or
Q40: Determine the area of a triangle having
Q71: Perform the indicated operation using the
Q72: Perform the operation and leave the
Q73: The vector <span class="ql-formula" data-value="\mathbf
Q74: The vector <span class="ql-formula" data-value="\mathbf
Q76: Find the component form of v
Q78: In the figure, <span class="ql-formula"
Q79: Find a unit vector in the
Q80: Represent the complex number graphically, and