The Linear Programming Problem Has an Unusual Characteristic

Multiple Choice

The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the maximum value of the objective function (if possible) and where it occurs. ​
Objective function:
​
Z = x + y
​
Constraints:
​
X ≥ 0
Y ≥ 0
-x + y ≤ 1
-x + 5y ≤ 7
​

A) 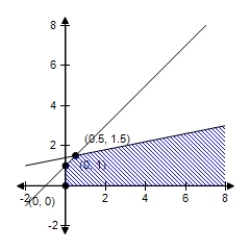Maximum at (0.5, 1.5) : 2
B) 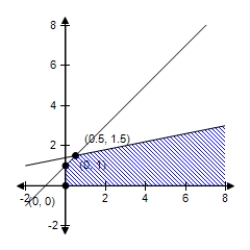The region determined by the constraints is unbounded. For this unbounded region, there is no maximum value of z.
C) Maximum at (0, 1) : 1
D) 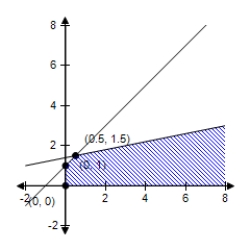Maximum at (0, 0) : 0
E) 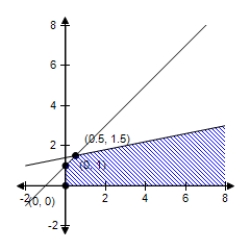Maximum at (1.5, 0.5) : 2