Select the Graph of the Polar Equation Using Symmetry, Zeros $r = 2$

Multiple Choice

Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
$r = 2$

A) Symmetric with respect to $\theta = \frac { \pi } { 2 }$ , polar axis, poleCircle with radius 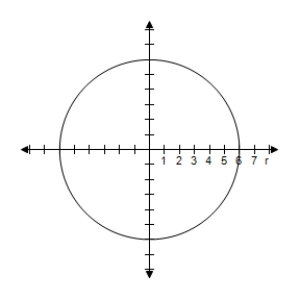$r = 2$
B) Symmetric with respect to $\theta = \frac { \pi } { 2 }$ , polar axis, poleCircle with radius 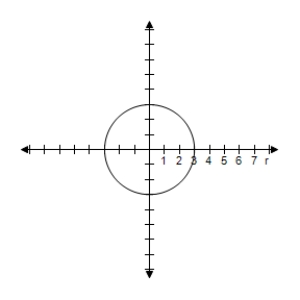$r = 2$
C) Symmetric with respect to $\theta = \frac { \pi } { 2 }$ , polar axis, poleCircle with radius 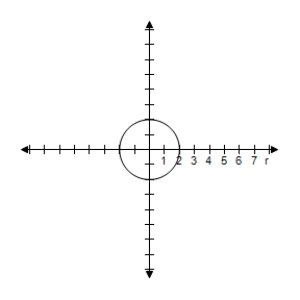$r = 2$
D) Symmetric with respect to $\theta = \frac { \pi } { 2 }$ , polar axis, poleCircle with radius $r = 2$
E) Symmetric with respect to $\theta = \frac { \pi } { 2 }$ , polar axis, poleCircle with radius $r = 2$