Multiple Choice
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
A) Symmetric with respectto the polar axis, , and the poleLemniscate 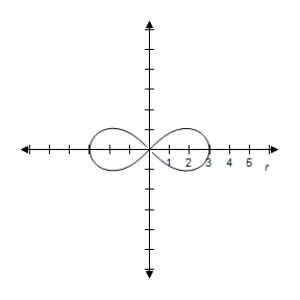
B) Symmetric with respectto the polar axis, , and the poleLemniscate 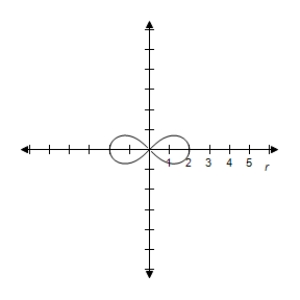
C) Symmetric with respectto the polar axis, , and the poleLemniscate 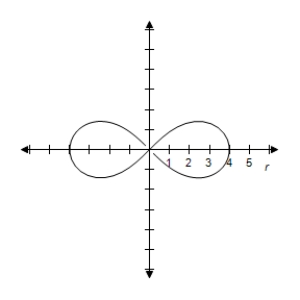
D) Symmetric with respectto the polar axis, , and the poleLemniscate 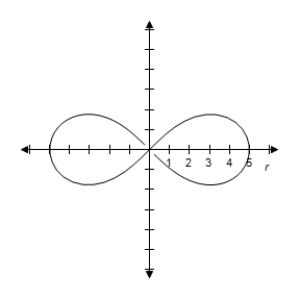
E) Symmetric with respectto the polar axis, , and the poleLemniscate 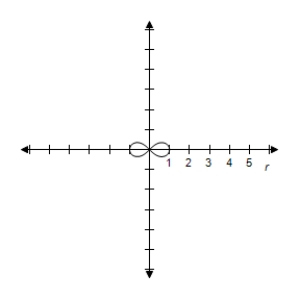
Correct Answer:

Verified
Correct Answer:
Verified
Q169: Find the center and vertices of
Q170: Find the inclination <span class="ql-formula"
Q171: Select the correct equation of the
Q172: Eliminate the parameter and write the
Q173: Find the inclination <span class="ql-formula"
Q175: Select the graph of the polar
Q176: Find the distance between the point
Q177: Write the equation of the ellipse
Q178: Find the center and the vertices
Q179: Select the graph of the equation