Multiple Choice
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
A) Symmetric with respect to 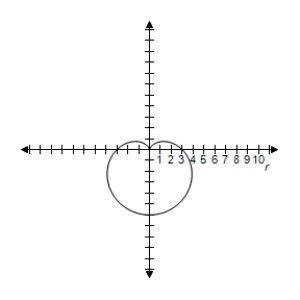
B) Symmetric with respect to 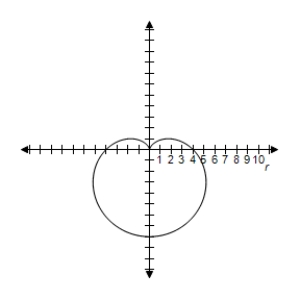
C) Symmetric with respect to 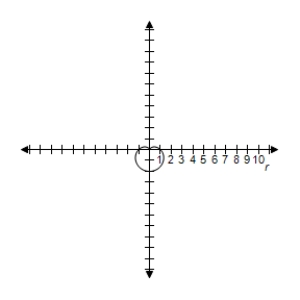
D) Symmetric with respect to 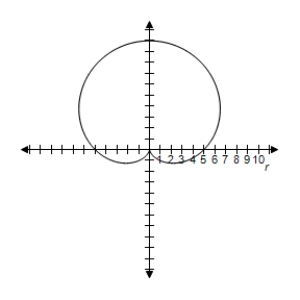
E) Symmetric with respect to 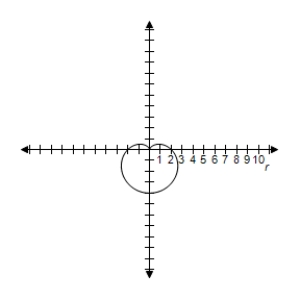
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q262: Find the equation of the hyperbola
Q263: Find a polar equation of the
Q264: Find the center and vertices of
Q265: Sketch the graph of the ellipse,
Q266: Graph the following equation.
Q268: Find a polar equation of the
Q269: Using following result find a set
Q270: Convert the polar equation to rectangular
Q271: Find the standard form of the
Q272: Use the Quadratic Formula to solve