Multiple Choice
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
A) Symmetric with respect to 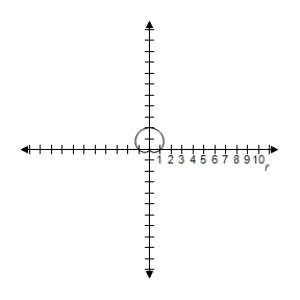
B) Symmetric with respect to 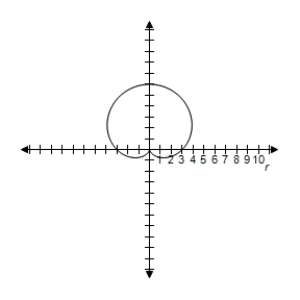
C) Symmetric with respect to 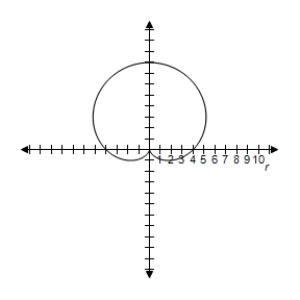
D) Symmetric with respect to 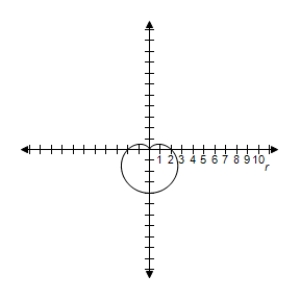
E) Symmetric with respect to 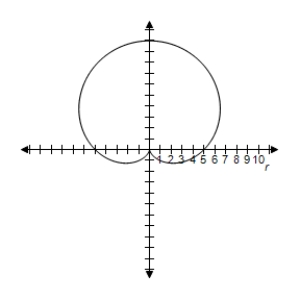
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q26: Find the standard form of the equation
Q447: A point in rectangular coordinates is
Q448: Use the discriminant to classify the
Q449: Find the center and foci of
Q450: Select the graph of the equation.
Q451: A point in rectangular coordinates is
Q453: Find the vertex, focus, and directrix
Q454: Identify the equation as a circle,
Q455: Find the angle <span class="ql-formula"
Q456: Select the correct graph of the