Solved

Select the Correct Graph of the Polar Equation r=74r = \frac { 7 } { 4 }

Question 12

Multiple Choice

Select the correct graph of the polar equation.Describe your viewing window. r=74r = \frac { 7 } { 4 }


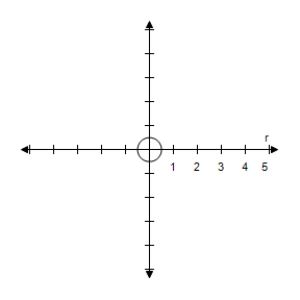
A) Select the correct graph of the polar equation.Describe your viewing window. r = \frac { 7 } { 4 } A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−5Xmax⁡=5Xscl=1Ymin⁡=−5Ymax⁡=5Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 5 \\X _ { \max } = 5 \\X _ { s c l } = 1 \\Y _ { \min } = - 5 \\Y _ { \max } = 5 \\Y _ { s c l } = 1\end{array}
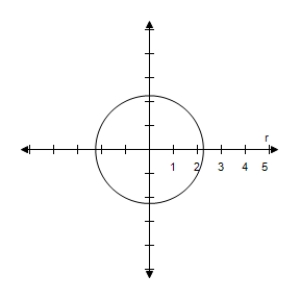
B) Select the correct graph of the polar equation.Describe your viewing window. r = \frac { 7 } { 4 } A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−5Xmax⁡=5Xscl=1Ymin⁡=−5Ymax⁡=5Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 5 \\X _ { \max } = 5 \\X _ { s c l } = 1 \\Y _ { \min } = - 5 \\Y _ { \max } = 5 \\Y _ { s c l } = 1\end{array}
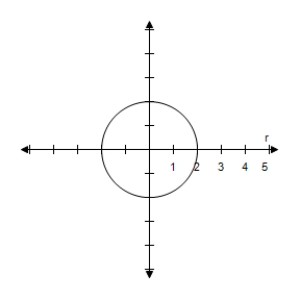
C) Select the correct graph of the polar equation.Describe your viewing window. r = \frac { 7 } { 4 } A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−5Xmax⁡=5Xscl=1Ymin⁡=−5Ymax⁡=5Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 5 \\X _ { \max } = 5 \\X _ { s c l } = 1 \\Y _ { \min } = - 5 \\Y _ { \max } = 5 \\Y _ { s c l } = 1\end{array}
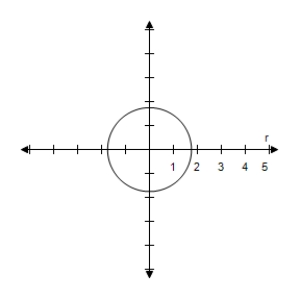
D) Select the correct graph of the polar equation.Describe your viewing window. r = \frac { 7 } { 4 } A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−5Xmax⁡=5Xscl=1Ymin⁡=−5Ymax⁡=5Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 5 \\X _ { \max } = 5 \\X _ { s c l } = 1 \\Y _ { \min } = - 5 \\Y _ { \max } = 5 \\Y _ { s c l } = 1\end{array}
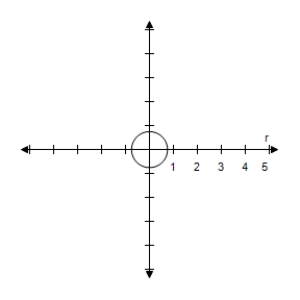
E) Select the correct graph of the polar equation.Describe your viewing window. r = \frac { 7 } { 4 } A) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} B) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} C) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} D) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} E) \begin{array} { l } \theta _ { \min } = 0 \\ \theta _ { \max } = 2 \pi \\ \theta _ { s t e p } = \pi / 24 \\ X _ { \min } = - 5 \\ X _ { \max } = 5 \\ X _ { s c l } = 1 \\ Y _ { \min } = - 5 \\ Y _ { \max } = 5 \\ Y _ { s c l } = 1 \end{array} θmin⁡=0θmax⁡=2πθstep=π/24Xmin⁡=−5Xmax⁡=5Xscl=1Ymin⁡=−5Ymax⁡=5Yscl=1\begin{array} { l } \theta _ { \min } = 0 \\\theta _ { \max } = 2 \pi \\\theta _ { s t e p } = \pi / 24 \\X _ { \min } = - 5 \\X _ { \max } = 5 \\X _ { s c l } = 1 \\Y _ { \min } = - 5 \\Y _ { \max } = 5 \\Y _ { s c l } = 1\end{array}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q7: The equations of a parabola and

Q8: Find the vertex and focus of

Q9: Select the graph of degenerate conic.

Q10: Describe the graph of the polar

Q11: Convert the rectangular equation to polar

Q13: Find the vertex, focus, and directrix

Q14: Find the distance between the point

Q15: Find the center, vertices and foci

Q16: Convert the rectangular equation to polar

Q17: Find the vertex and focus of